Codeforces Round #282 (Div. 1)B. Obsessive String KMP+DP

B. Obsessive String

 

Hamed has recently found a string t and suddenly became quite fond of it. He spent several days trying to find all occurrences of t in other strings he had. Finally he became tired and started thinking about the following problem. Given a string s how many ways are there to extract k ≥ 1 non-overlapping substrings from it such that each of them contains string t as a substring? More formally, you need to calculate the number of ways to choose two sequences a1, a2, ..., ak and b1, b2, ..., bk satisfying the following requirements:

• k ≥ 1
• 
• 
• 
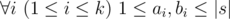
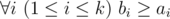
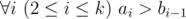
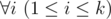•   t is a substring of string saisai + 1... sbi (string s is considered as 1-indexed).

As the number of ways can be rather large print it modulo 109 + 7.

Input

Input consists of two lines containing strings s and t (1 ≤ |s|, |t| ≤ 105). Each string consists of lowercase Latin letters.

Output

Print the answer in a single line.

Examples

input

ababa
aba

output

5

 

题意：

给两个串S,T，问能找出多少的S的(a1,b1)(a2,b2)..(ak,bk)，使Sa1---Sb1,...Sak---Sbk都包含子串T，其中k>=1,且(a1,b1)...(ak,bk)互不相交。

题解：

　　kmp预处理匹配点。。。

　　f[i]表示前i个的合法划分数。。

　　f[i]=f[i–1] （表示将最后一个舍弃）

　　sum[i]=∑ f[k] (k<=i)

　　设上一个匹配点为last

　　f[i]+=sum[last–1]+last

　　即有两种情况

　　[1….L-1(这部分任意，只要合法，允许舍弃末尾）] [L…i] 这样划分

　　或者直接 k=1 即只有一个划分[L…i]

　　L<=last

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>
#include<vector>
using namespace std;
const int N = 1e5+, M = , mod = , inf = 0x3f3f3f3f;
typedef long long ll;
//不同为1，相同为0

ll next[N],dp[N],f[N],sum[N];
char s[N],t[N];
int main() {
    scanf("%s%s",t+,s+);
    int n = strlen(t+),m = strlen(s+);
    int k = ;
    for(int i=;i<=m;i++) {
        while(k>&&s[k+]!=s[i]) k = next[k];
        if(s[k+]==s[i])k++;
        next[i] = k;
    }
    k = ;
    for(int i=;i<=n;i++) {
        while(k>&&s[k+]!=t[i]) k = next[k];
        if(s[k+]==t[i]) k++;
        if(k==m) k = next[k],f[i] = ;
    }
    int last = -;
    for(int i=;i<=n;i++) {
        dp[i] = dp[i-];
        if(f[i]) last = i-m+;
        if(last!=-) dp[i]+=sum[last-]+last;
        sum[i] = sum[i-]+dp[i];
        dp[i]%=mod,sum[i]%=mod;
    }
    cout<<dp[n]<<endl;
}