[WC2011]最大XOR和路径（线性基）

P4151 [WC2011]最大XOR和路径

题目描述

XOR（异或）是一种二元逻辑运算，其运算结果当且仅当两个输入的布尔值不相等时才为真，否则为假。 XOR 运算的真值表如下（ 1 表示真， 0 表示假）：

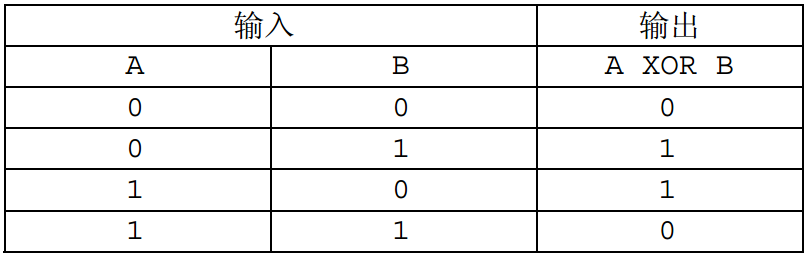
而两个非负整数的 XOR 是指将它们表示成二进制数，再在对应的二进制位进行 XOR 运算。

譬如 12 XOR 9 的计算过程如下：

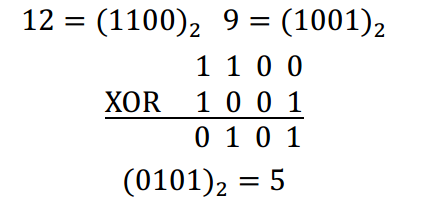
故 12 XOR 9 = 5 。

容易验证， XOR 运算满足交换律与结合律，故计算若干个数的 XOR 时，不同的计算顺序不会对运算结果造成影响。从而，可以定义 KK 个非负整数 \(A_1\),\(A_2\)​ ,\(……\) , \(A_{K-1}\)​,\(A_K\)的 XOR 和为

\(A_1\) XOR \(A_2\) XOR …… XOR \(A_{K-1}\) XOR \(A_K\)

考虑一个边权为非负整数的无向连通图，节点编号为 1 到 N ，试求出一条从 1 号节点到 N 号节点的路径，使得路径上经过的边的权值的 XOR 和最大。

路径可以重复经过某些点或边，当一条边在路径中出现了多次时，其权值在计算 XOR 和时也要被计算相应多的次数，具体见样例。

输入输出格式

输入格式：

输入文件 xor.in 的第一行包含两个整数 \(N\) 和 \(M\) ， 表示该无向图中点的数目与边的数目。

接下来 M 行描述 M 条边，每行三个整数 \(S_i\)​ ， \(T_i\)​ ， \(D_i\) ， 表示 \(S_i\) 与 \(T_i\) 之间存在一条权值为 \(D_i\) 的无向边。

图中可能有重边或自环。

输出格式：

输出文件 xor.out 仅包含一个整数，表示最大的 XOR 和（十进制结果）。

输入输出样例

输入样例#1： 复制

5 7

1 2 2

1 3 2

2 4 1

2 5 1

4 5 3

5 3 4

4 3 2

输出样例#1： 复制

6

说明

【样例说明】

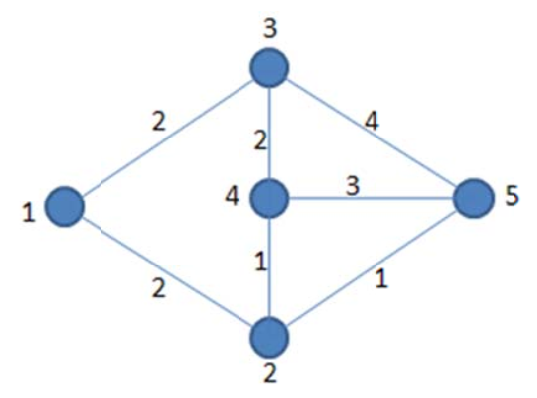
如图，路径 \(1 \rightarrow 2 \rightarrow 4 \rightarrow 3 \rightarrow 5 \rightarrow 2 \rightarrow 4 \rightarrow 5\)对应的XOR和为

2 XOR 1 XOR 2 XOR 4 XOR 1 XOR 1 XOR 3=6

当然，一条边数更少的路径 \(1 \rightarrow 3 \rightarrow 5\) 对应的XOR和也是 2 XOR 4 = 6 。

【数据规模】

对于 \(20 \%\) 的数据， \(N \leq 100\) ， \(M \leq 1000\) ， \(D_i\) \(\leq\) \(10^{4}\) ；

对于 \(50 \%\) 的数据， \(N \leq 1000\) ， \(M \leq 10000\) ， \(D_i\) \(\leq\) \(10^{18}\) ；

对于 \(70 \%\) 的数据， \(N \leq 5000\) ， \(M\) \(\leq\) \(50000\) ， \(D_i\) \(\leq\) \(10^{18}\) ；

对于 \(100 \%\) 的数据， \(N \leq 50000\) ， \(M \leq 100000\) ， \(D_i \leq 10^{18}\) 。

---

题解

怎么说呢。有这样一条定理

（不知道这个之前的我根本不会做这道题）

• 任意一条 \(1\) 到 \(n\) 的路径的异或和，都可以由任意一条 \(1\) 到 \(n\) 路径的异或和与图中的一些环的异或和来组合得到。

为什么？

如果我们走一条路径的话，如果路径上存在一个环，那么这个环的总异或值就可以下放到线性基。因为把这个环走两遍就等于没走这个环，同样我如果是由一条路径到的这个环，沿原路返回，那等于那条路径没走，只走了环。

在这种条件下，我们可以考虑把环储存为一个线性基的元素。因为这个元素是可选和可不选的。

那么为什么是任意的简单路径呢?

因为 \(1\) 到 \(N\) 的简单路径是必须要走的。这显然。

然后如果有多条 \(1\) 到 \(N\) 的路径，那么这显然也构成一个环，也是可以抵消异或的任意一条其他的路径的是吧。

然后这个题目就好做了咕咕咕。

---

代码

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<cmath>
#define ll long long
using namespace std;
ll dis[50001],sum[101],b[101];
ll n,m,vis[50001];
int head[100001],num;
struct node{
    int next,to;
    ll v;
}e[100001<<1];

ll read()
{
    ll x=0,w=1;char ch=getchar();
    while(ch>'9'||ch<'0'){if(ch=='-')w=-1;ch=getchar();}
    while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
    return x*w;
}

void add(int from,int to,ll v){
    num++;
    e[num].to=to;
    e[num].v=v;
    e[num].next=head[from];
    head[from]=num;
}

void update(ll x){
    for(int i=60;i>=0;i--){
        if(sum[i]&x){
            if(b[i])x^=b[i];
            else {
                b[i]=x;
                break;
            }
        }
    }
}

void dfs(int x){
    vis[x]=1;
    for(int i=head[x];i;i=e[i].next){
        int v=e[i].to;
        if(vis[v])update(dis[v]^e[i].v^dis[x]);
        else dis[v]=dis[x]^e[i].v,dfs(v);
    }
}

ll query(ll x){
    ll ans=x;
    for(int i=60;i>=0;i--){
        if((ans^b[i])>ans)ans^=b[i];
    }
    return ans;
}

int main()
{
    n=read();m=read();
    sum[0]=1;for(int i=1;i<=60;i++)sum[i]=sum[i-1]*2;
    for(int i=1;i<=m;i++){
        ll x=read(),y=read(),z=read();
        add(x,y,z);add(y,x,z);
    }
    dfs(1);
    printf("%lld",query(dis[n]));
    return 0;
}