吴恩达机器学习笔记（八） —— 降维与主成分分析法(PCA)

主要内容：

一.降维与PCA

二.PCA算法过程

三.PCA之恢复

四.如何选取维数K

五.PCA的作用与适用场合

一.降维与PCA

1.所谓降维，就是将数据由原来的n个特征(feature)缩减为k个特征(可能从n个中直接选取k个，也能根据这n个重新组合成k个)。可起到数据压缩的作用（因而也就存在数据丢失）。

2.PCA，即主成分分析法，属于降维的一种方法。其主要思想就是：根据原始的n个特征（也就是n维），重新组合出k个特征，且这k个特征能最大量度地涵盖原始的数据信息（虽然会导致信息丢失）。有一个结论：当某一维的方差越大时，其所包含的信息量也越大，表明其越重要；反之则反。所以，PCA的主要工作就是：重构出k个特征，使其所包含的信息量最大。

3.以下两个例子：

第一幅图：将平面上（二维）的点映射到一直线或向量上（一维），其丢失的信息量就是：每个点到直线上的距离。因为降维之后，就认为所有点都在直线上了。同理第二幅图将空间上投影到一个平面上。注意：这两个例子都选取了与原始数据尽可能“靠近”的直线或者平面，使得其保存下来的信息量最大。

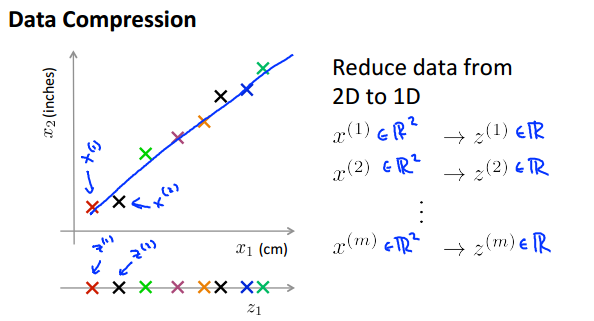
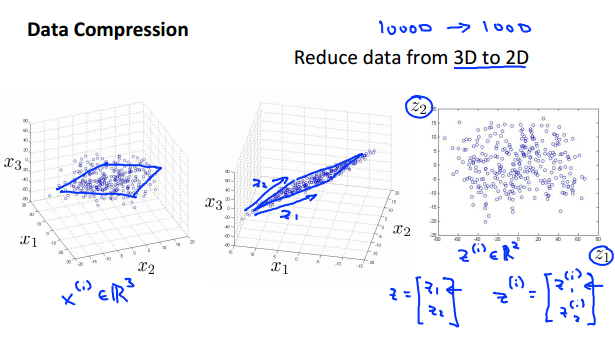
二.PCA算法过程

1.首先，需要对数据特征进行归一化

2.求出特征的协方差矩阵

3.求出协方差矩阵的特征值及特征向量，这里可直接调用函数库

其中，S为对角矩阵，其对角线上的数就是协方差矩阵的特征值，而U就是协方差矩阵的特征向量。

而U的前k列就是我们要求的新特征（用于代替原来的n个特征，起到数据压缩的作用）。

所以，假设原始的数据特征为x（n维），经过用变换后变为z（k维），则有如下公式：

综上，PCA算法可总结为：

 注：至于为什么要用到协方差矩阵，以及为什么要求特征向量等等一系列数学问题，这篇博客：PCA算法原理:为什么用协方差矩阵 可以很好地解释。

（自己还没看懂，只有个感性的认识）

三.PCA之恢复

1.对人脸图像进行降维压缩的效果如下：

            （这里只取了部分）

2.那么压缩后，是否可以再还原了？是可以的，只是在压缩时丢失的那部分数据找不回来了。恢复方式如下：

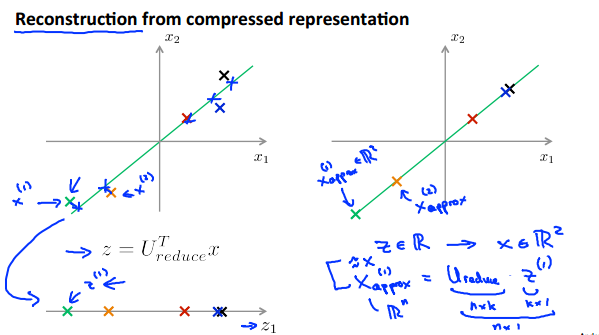
即：X(approx) = U(reduce) * Z

由图像可知：恢复后，所有的点后落在了直线上，所以丢失的数据即为原始点与直线的距离。

四.如何选取维数K

如果可能，k当然越小越好，k越小表明压缩的程度越高，但同时又要保证足够多的数据量。因此，选出最小的k，满足：

以下为其求解求解过程，并且我们可以直接调用函数库：

五.PCA的作用与适用场合

1.PCA用甚好好处？或者说有哪些应用？

1) 可以减少内存空间

2) 可以对算法进行提速

3) 可以用于数据可视化

2.既然PCA这么好用？那是不是可以随便用呢？答案否：

个人认为，PCA其实是个辅助工具，用不用它，从功能上而言没有太大区别，其区别就在于性能。也就是说，在用线性回归或者Logistic回归做一些事情时，如果直接运行，其效果或者说性能都比价可观了，那就无谓使用PCA了。当出现占用内存过大，或者运算时间过长等，这时就可以利用PCA来提升一下算法的性能了。