Manacher's Algorithm 马拉车算法（最长回文串）

这个马拉车算法Manacher‘s Algorithm是用来查找一个字符串的最长回文子串的线性方法，由一个叫Manacher的人在1975年发明的，这个方法的最大贡献是在于将时间复杂度提升到了线性，这是非常了不起的。对于回文串想必大家都不陌生，就是正读反读都一样的字符串，比如 "bob", "level", "noon" 等等，那么如何在一个字符串中找出最长回文子串呢，可以以每一个字符为中心，向两边寻找回文子串，在遍历完整个数组后，就可以找到最长的回文子串。但是这个方法的时间复杂度为O(n*n)，并不是很高效，下面我们来看时间复杂度为O(n)的马拉车算法。

由于回文串的长度可奇可偶，比如"bob"是奇数形式的回文，"noon"就是偶数形式的回文，马拉车算法的第一步是预处理，做法是在每一个字符的左右都加上一个特殊字符，比如加上'#'，那么

bob    -->    #b#o#b#

noon    -->    #n#o#o#n#

这样做的好处是不论原字符串是奇数还是偶数个，处理之后得到的字符串的个数都是奇数个，这样就不用分情况讨论了，而可以一起搞定。接下来我们还需要和处理后的字符串t等长的数组p，其中p[i]表示以t[i]字符为中心的回文子串的半径，若p[i] = 1，则该回文子串就是t[i]本身，那么我们来看一个简单的例子：

# 1 # 2 # 2 # 1 # 2 # 2 #
1 2 1 2 5 2 1 6 1 2 3 2 1

由于第一个和最后一个字符都是#号，且也需要搜索回文，为了防止越界，我们还需要在首尾再加上非#号字符，实际操作时我们只需给开头加上个非#号字符，结尾不用加的原因是字符串的结尾标识为'\0'，等于默认加过了。通过p数组我们就可以找到其最大值和其位置，就能确定最长回文子串了，那么下面我们就来看如何求p数组，需要新增两个辅助变量mx和id，其中id为最大回文子串中心的位置，mx是回文串能延伸到的最右端的位置，这个算法的最核心的一行如下：

p[i] = mx > i ? min(p[2 * id - i], mx - i) : 1;

可以这么说，这行要是理解了，那么马拉车算法基本上就没啥问题了，那么这一行代码拆开来看就是

如果mx > i, 则 p[i] = min(p[2 * id - i], mx - i)

否则， p[i] = 1

当 mx - i > P[j] 的时候，以S[j]为中心的回文子串包含在以S[id]为中心的回文子串中，由于 i 和 j 对称，以S[i]为中心的回文子串必然包含在以S[id]为中心的回文子串中，所以必有 P[i] = P[j]，见下图。

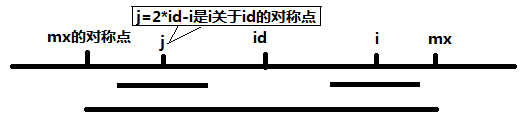
当 P[j] >= mx - i 的时候，以S[j]为中心的回文子串不一定完全包含于以S[id]为中心的回文子串中，但是基于对称性可知，下图中两个绿框所包围的部分是相同的，也就是说以S[i]为中心的回文子串，其向右至少会扩张到mx的位置，也就是说 P[i] >= mx - i。至于mx之后的部分是否对称，就只能老老实实去匹配了。

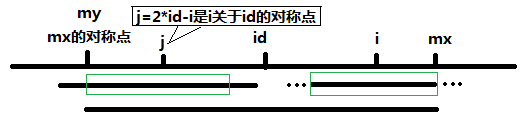
对于 mx <= i 的情况，无法对 P[i]做更多的假设，只能P[i] = 1，然后再去匹配了。

参见如下实现代码：

#include <vector>
#include <iostream>
#include <string>

using namespace std;

string Manacher(string s) {
    // Insert '#'
    string t = "$#";
    for (int i = 0; i < s.size(); ++i) {
        t += s[i];
        t += "#";
    }
    // Process t
    vector<int> p(t.size(), 0);
    int mx = 0, id = 0, resLen = 0, resCenter = 0;
    for (int i = 1; i < t.size(); ++i) {
        p[i] = mx > i ? min(p[2 * id - i], mx - i) : 1;
        while (t[i + p[i]] == t[i - p[i]]) ++p[i];
        if (mx < i + p[i]) {
            mx = i + p[i];
            id = i;
        }
        if (resLen < p[i]) {
            resLen = p[i];
            resCenter = i;
        }
    }
    return s.substr((resCenter - resLen) / 2, resLen - 1);
}

int main() {
    string s1 = "12212";
    cout << Manacher(s1) << endl;
    string s2 = "122122";
    cout << Manacher(s2) << endl;
    string s = "waabwswfd";
    cout << Manacher(s) << endl;
}