剑指Offer的学习笔记（C#篇）-- 斐波那契数列

题目：大家都知道斐波那契数列，现在要求输入一个整数n，请你输出斐波那契数列的第n项（从0开始，第0项为0）。

一 . 理解概念

斐波那契数列概念：斐波那契数列（Fibonacci sequence），又称黄金分割数列，因数学家列昂纳多·斐波那契（Leonardoda Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”（来自百度百科）。具体可由以下公式表示：

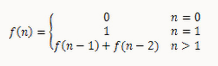
二.C#代码如何实现

由上述公式可知，斐波那契数列存在两个特殊值，即当n=0和n=1时，因此，可将n等于0与1时提出来作单独处理，而剩下的部分再作单独处理，基于这种想法，实现该目标可使用两种方法：

方法1：递归法。

斐波那契数列是递归法最典型的一种体现，但又存在着很多的不足。

其中，递归的实现是通过调用函数本身，函数调用的时候，每次调用时要做地址保存，参数传递等，这是通过一个递归工作栈实现的。具体是每次调用函数本身要保存的内容包括：局部变量、形参、调用函数地址、返回值。那么，如果递归调用 N 次，就要分配 N*局部变量、N*形参、N*调用函数地址、N*返回值，这势必是影响效率的，该题目中，用递归方法计算的时间复杂度是以n的指数的方式递增的，此段来自Edison Zhou的博文。

如下代码是使用递归实现的斐波那契数列（该题目中可以看出，若你>1,计算f(n)需要不断重新的调用Fibonacci函数）：

class Solution{
     public int Fibonacci(int n)
    {
        //当n小于等于0时，返回0
        if (n <= )
        {
            return ;
        }
        //当n等于1时，返回1
        if (n == )
        {
            return ;
        }
        //否则，返回前两个数之和
        else
       {
             return Fibonacci(n - ) + Fibonacci(n - );
        }
    }
}

很显然，递归虽然可以实现斐波那契数列，但却存在着一定的问题。

方法二 ： 循环法。

由于递归存在着效率低问题，为解决该问题，引入循环的方法避免了递归法重复计算的弊端，从而运算的时间复杂度变为是O(n)。

具体实现代码如下：

class Solution
{
    public int Fibonacci(int n)
    {
        // write code here
        int x = ;
        int y = ;
        int result = ;
        if (n == )
        {
            return ;
        }
        if (n == )
        {
            return ;
        }
        else
        {
            for (int i=;i<=n;i++)
        {
            result = x + y;
            x = y;
            y = result;
        }
            return result;
        }
    }
}

上述代码在实现上与递归法大同小异，不同点在于不需要重复的调用函数，个人感觉理解起来更加容易一点。