python 图像的离散傅立叶变换

　　图像(MxN)的二维离散傅立叶变换可以将图像由空间域变换到频域中去，空间域中用x,y来表示空间坐标，频域由u,v来表示频率，二维离散傅立叶变换的公式如下：

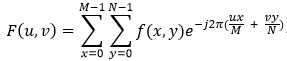
　　在python中，numpy库的fft模块有实现好了的二维离散傅立叶变换函数，函数是fft2，输入一张灰度图，输出经过二维离散傅立叶变换后的结果，但是具体实现并不是直接用上述公式，而是用快速傅立叶变换。结果需要通过使用abs求绝对值才可以进行可视化，但是视觉效果并不理想，因为傅立叶频谱范围很大，所以要用log对数变换来改善视觉效果。

　　在使用log函数的时候，要写成log(1 + x) 而不是直接用log(x),这是为了避开对0做对数处理。

　　另外，图像变换的原点需要移动到频域矩形的中心，所以要对fft2的结果使用fftshift函数。最后也可以使用log来改善可视化效果。

　　代码如下：

 import numpy as np
 import matplotlib.pyplot as plt

 img = plt.imread('photo.jpg')

 #根据公式转成灰度图
 img = 0.2126 * img[:,:,0] + 0.7152 * img[:,:,1] + 0.0722 * img[:,:,2]

 #显示原图
 plt.subplot(231),plt.imshow(img,'gray'),plt.title('original')

 #进行傅立叶变换，并显示结果
 fft2 = np.fft.fft2(img)
 plt.subplot(232),plt.imshow(np.abs(fft2),'gray'),plt.title('fft2')

 #将图像变换的原点移动到频域矩形的中心，并显示效果
 shift2center = np.fft.fftshift(fft2)
 plt.subplot(233),plt.imshow(np.abs(shift2center),'gray'),plt.title('shift2center')

 #对傅立叶变换的结果进行对数变换，并显示效果
 log_fft2 = np.log(1 + np.abs(fft2))
 plt.subplot(235),plt.imshow(log_fft2,'gray'),plt.title('log_fft2')

 #对中心化后的结果进行对数变换，并显示结果
 log_shift2center = np.log(1 + np.abs(shift2center))
 plt.subplot(236),plt.imshow(log_shift2center,'gray'),plt.title('log_shift2center')

　　运行结果：

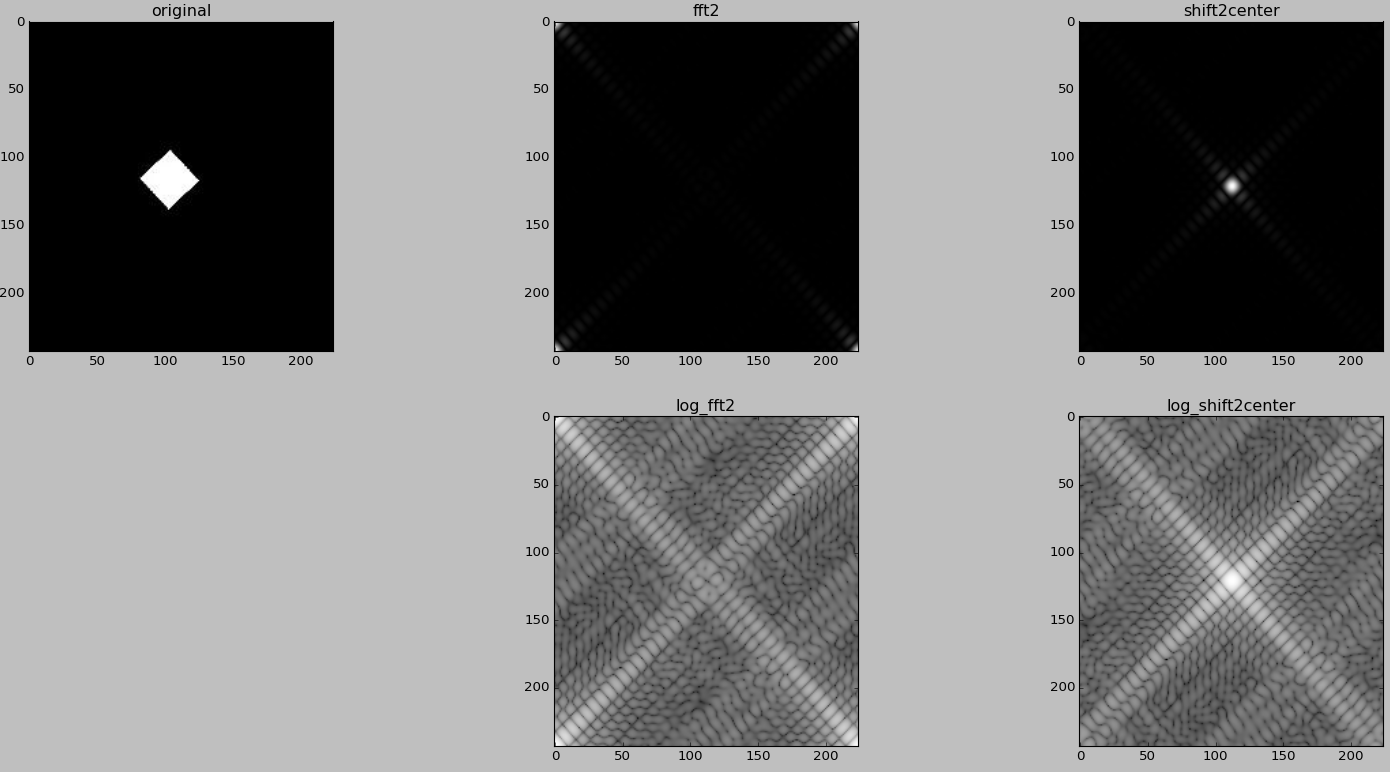
　　 根据公式实现的二维离散傅立叶变换如下：

 import numpy as np
 import matplotlib.pyplot as plt
 PI = 3.141591265
 img = plt.imread('temp.jpg')

 #根据公式转成灰度图
 img = 0.2126 * img[:,:,0] + 0.7152 * img[:,:,1] + 0.0722 * img[:,:,2]

 #显示原图
 plt.subplot(131),plt.imshow(img,'gray'),plt.title('original')

 #进行傅立叶变换，并显示结果
 fft2 = np.fft.fft2(img)
 log_fft2 = np.log(1 + np.abs(fft2))
 plt.subplot(132),plt.imshow(log_fft2,'gray'),plt.title('log_fft2')

 h , w = img.shape
 #生成一个同样大小的复数矩阵
 F = np.zeros([h,w],'complex128')
 for u in range(h):
     for v in range(w):
         res = 0
         for x in range(h):
             for y in range(w):
                 res += img[x,y] * np.exp(-1.j * 2 * PI * (u * x / h + v * y / w))
         F[u,v] = res
 log_F = np.log(1 + np.abs(F))
 plt.subplot(133),plt.imshow(log_F,'gray'),plt.title('log_F')

　　直接根据公式实现复杂度很高，因为是四重循环，时间复杂度为O(M²N²)，所以实际用的时候需要用快速傅立叶变换来实现

参考

1、https://www.cnblogs.com/xianglan/archive/2010/12/30/1922386.html