CNN中感受野的理解

---

本文摘自看完还不懂卷积神经网络“感受野”？那你来找我

作者：程序_小白
链接：https://www.jianshu.com/p/9305d31962d8

---

一、到底什么是“感受野”（接受野Receptive Field）

感受野是一个神经元对原始图像的连接

通常说：第几层对输入数据（即原始图像）的感受野

二、图解说明

为了更好地说明整个卷积神经网络的工作过程，下面以一个例子说明，原始图像的大小为10x10，一共设计了5个网络层，前面4个是卷积层，卷积核的大小为3x3，最后一个是池化层，大小为2x2,为了较简单的说明，本次所有的步幅stride均为1.

注意：感受野在计算的时候不考虑“边界填充”，因为填充的边界已经不是原始图像本身的内容了，感受野描述的是输出特征到原始图像的映射关系，故而不考虑padding 。实际建模过程中可能需要填充边界，原理一样，只是计算稍微复杂点。

1、第一次卷积运算

 

 

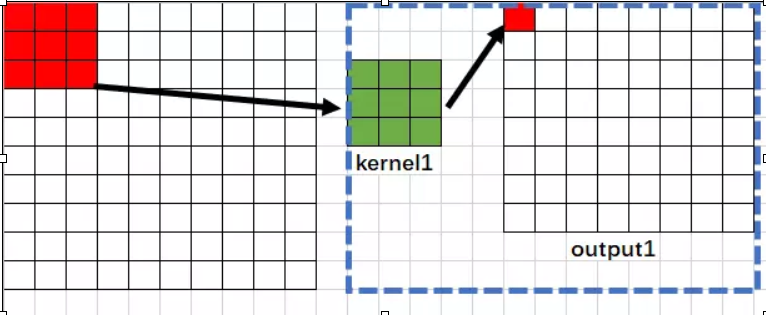
从上面可以看出：第一层网络输出的图像中，输出结果为8x8，output1输出的每一个特征（即每一个像素）受到原始图像的3x3区域内的影响，故而第一层的感受野为3，用字母表示为

RF1=3   （每一个像素值与原始图像的3x3区域有关）

2、第二次卷积运算

 

 

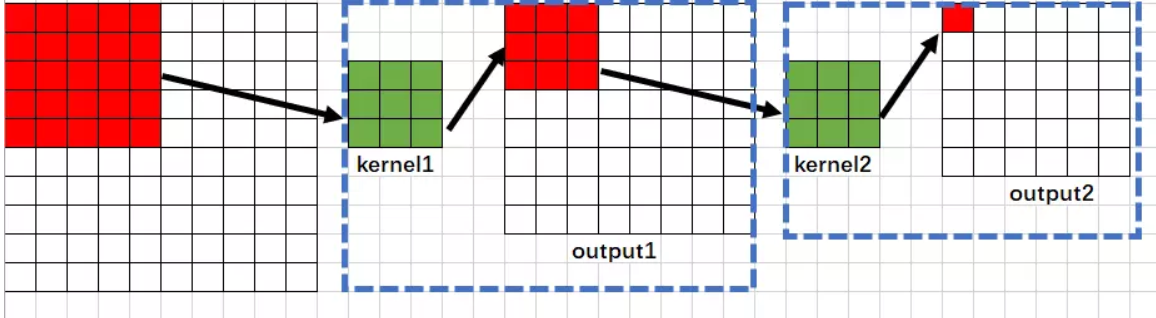
从上图可以看出，经历两次卷积运算之后，最终的输出图像为6x6，output2输出的每一个特征（即每一个像素）受到output1的范围影响为3x3，而output1中的这个3x3又收到原始图像的5x5的范围的影响，故而第二层的感受野为5，即

RF2=5   （每一个像素值与原始图像的5x5区域有关）

3、第三次卷积运算

 

 

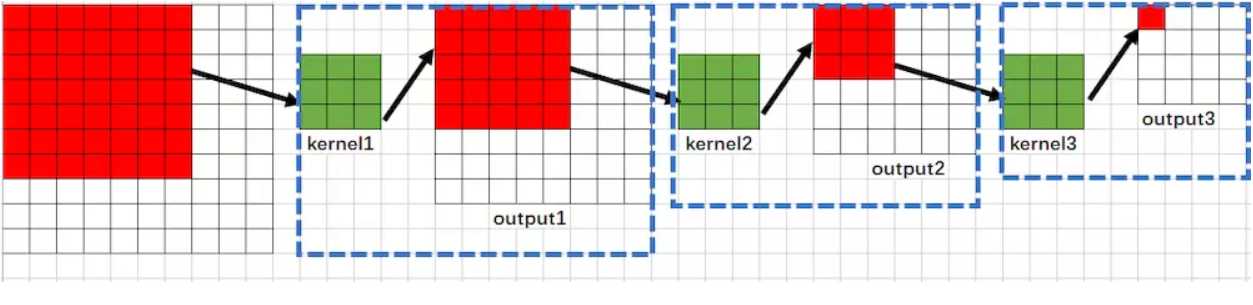
从上图可以看出，经历三次卷积运算之后，最终的输出图像为4x4，output3输出的每一个特征（即每一个像素）受到output2的范围影响为3x3，而output2中的这个3x3又受到output1的5x5的范围的影响，而output1中的这个5x5又受到原始图像的7x7的范围的影响，故而第三层的感受野为7，即

RF3=7   （每一个像素值与原始图像的7x7区域有关）

4、第四次卷积运算

 

 

从上图可以看出，经历四次卷积运算之后，最终的输出图像为2x2，output4输出的每一个特征（即每一个像素）受到output3的范围影响为3x3，而output3中的这个3x3又受到output2的5x5的范围的影响，而output2中的这个5x5又受到output1的7x7的范围的影响，而output1中的这个7x7又受到原始图形的9x9的范围的影响，故而第四层的感受野为9，即

RF4=9   （每一个像素值与原始图像的9x9区域有关）

5、第五次池化运算

 

 

从上图可以看出，经历四次卷积运算和一次池化运算之后，最终的输出图像为1x1，output5输出的每一个特征（即每一个像素）受到output4的范围影响为2x2，而output4中的这个2x2又受到output3的4x4的范围的影响，而output3中的这个4x4又受到output2的6x6的范围的影响，而output2中的这个6x6受到output1的8x8的范围的影响，而output1中的这个8x8受到原始图像的10x10的范围的影响，故而第五层的感受野为10，即

RF5=10  （每一个像素值与原始图像的10x10区域有关）

三、递推公式推导

从上面的过程可以看出，感受野的推导是一个递推的过程，下面将展示这一过程。

RF1=3            k1（第一层的感受野，永远等于第一个卷积核的尺寸大小）k表示第几个卷积层

RF2=5            k1 + (k2-1)                                                            RF1+ (k2-1)

RF3=7            k1 + (k2-1) + （k3-1)                                            RF2+ (k3-1)

RF4=9            k1 + (k2-1) + （k3-1)   + (k4-1)                             RF3+ (k4-1)

RF4=10          k1 + (k2-1) + （k3-1)   + (k4-1)    + (k5-1)             RF4+ (k5-1)

总结：从上面可以看出，感受野的大小的求解是一个不断第一的过程，因为第一层的每一个像素的感受野始终是第一个卷积核的大小，故而RF1总是最先确定，然后以此类推，逐步求出RF2、RF3、RF4、RF5……

但是上面的所有步长均为 1 ，如果每一次卷积运算的步长 stride 不为1呢，同理，这里直接给出递推公式：

RFn=RFn-1 + (kn-1)*stride_n

其中stride_n表示的是第n次卷积的移动步幅stride。

求解过程是从RF1开始的。