【leetcode】1028. Recover a Tree From Preorder Traversal

题目如下：

We run a preorder depth first search on the root of a binary tree.

At each node in this traversal, we output D dashes (where D is the depth of this node), then we output the value of this node.  (If the depth of a node is D, the depth of its immediate child is D+1.  The depth of the root node is 0.)

If a node has only one child, that child is guaranteed to be the left child.

Given the output S of this traversal, recover the tree and return its root.

Example 1:

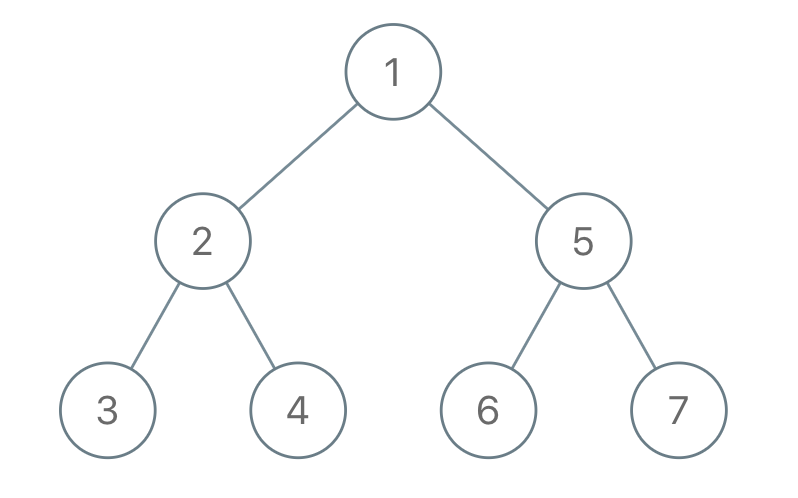
Input: "1-2--3--4-5--6--7"
Output: [1,2,5,3,4,6,7]

Example 2:

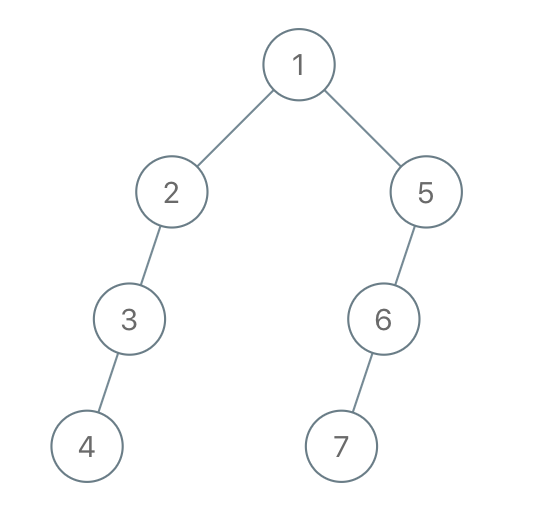
Input: "1-2--3---4-5--6---7"
Output: [1,2,5,3,null,6,null,4,null,7]

Example 3:

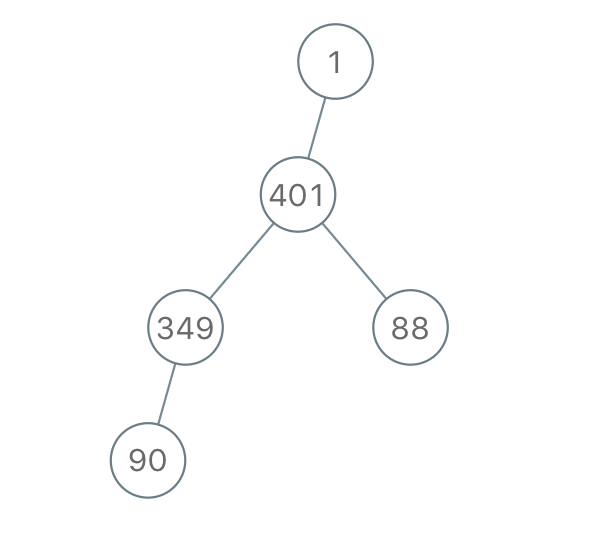
Input: "1-401--349---90--88"
Output: [1,401,null,349,88,90]

Note:

• The number of nodes in the original tree is between 1 and 1000.
• Each node will have a value between 1 and 10^9.

解题思路：本题就是DFS的思想。首先解析Input，得到每个数值所对应的层级，接下来把Input中每个元素创建成树的节点，并且依次存入stack中。每次从Input新取出一个元素，判断其层级是否是stack中最后一个元素的层级加1，如果是表示这个节点是stack中最后一个元素的左子节点；如果是stack中倒数第二个元素的层级加1，如果是表示这个节点是stack中倒数第二个元素的右子节点；如果都不满足，stack中最后一个元素出栈，再继续做如上判断，直到找出其父节点为止。

代码如下：

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution(object):
    def recoverFromPreorder(self, S):
        """
        :type S: str
        :rtype: TreeNode
        """
        queue = [[0]]
        dashCount = 0
        val = ''
        for i in S:
            if i == '-':
                if len(val) > 0:
                    queue[-1].insert(0,val)
                    val = ''
                dashCount += 1
            else:
                if dashCount > 0:
                    queue.append([dashCount])
                    dashCount = 0
                val += i
        queue[-1].insert(0, val)
        #print queue

        item = queue.pop(0)
        root = TreeNode(int(item[0]))
        nodeList = [[root,item[1]]]
        while len(queue) > 0:
            val,level = queue.pop(0)
            while len(nodeList) > 0:
                if level == nodeList[-1][1] + 1:
                    node = TreeNode(int(val))
                    nodeList[-1][0].left = node
                    nodeList.append([node,level])
                    break
                elif len(nodeList) >= 2 and level == nodeList[-2][1] + 1:
                    node = TreeNode(int(val))
                    nodeList[-2][0].right = node
                    nodeList.append([node, level])
                    break
                else:
                    nodeList.pop()
        return root