奇异值分解基础(SVD)

最近要了解一下Incremental PCA的一些知识，然后看到一篇论文里面讲到了SVD（奇异值分解），奈何自己以前没有把机器学习的课好好上，现在很多东西还是要补回来。所以，我就想了解一些SVD的基础知识。

PCA的实现一般有两种方法，一种是用特征值分解去实现，一种是用奇异值分解去实现的，SVD貌似在很多领域都有很重要的应用。

特征值和特征向量

特征值和特征向量是线性代数里面的基础知识，相信大部分人都知道：



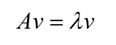
很显然，λ就是特征向量v对应的特征值，一个矩阵的一组特征向量都是相互正交的，相信这些大家在线性代数都有学习。特征值分解是将一个矩阵以下面的形式进行分解：



其中Q是这个矩阵A的特征向量组成的矩阵，Σ是一个对角矩阵，每一个对角线上的元素就是一个特征值。

特征值分解可以得到特征值和特征向量，特征值表示的是这个特征值的重要性，而特征向量表示的是这个特征是什么，可以将每一个特征向量理解为一个线性的子空间。不过特征值分解也有很多的局限，比如变换的矩阵必须是方阵。

奇异值

特征值分解只能针对于方阵，局限性较大，而奇异值分解是一个能够用于任意的矩阵的一种分解方法：



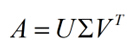
假设A是一个N*M的矩阵，那么U是一个N*N的方阵（里面的向量是正交的，U里面的向量称为左奇异向量），Σ是一个N*M的矩阵（除了对角线的元素都是0，对角线上的元素称为奇异值），V’（V的转置矩阵）是一个N*N的矩阵，里面的向量也是正教的，称为右奇异向量。



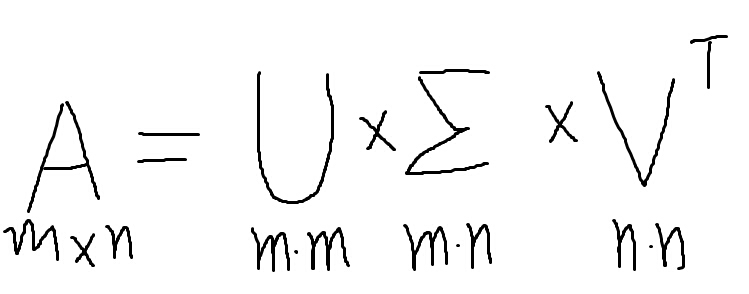
我们将矩阵A和他的转置矩阵相乘，就可以得到一个方阵，我们利用方阵的求特征值可以得到：



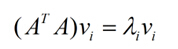
这里面的v，就是我们上面所说的右奇异向量，由此我们可以得到



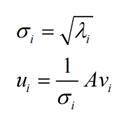
这里的σ就是上面所说的奇异值，u就是上面说的左奇异向量。奇异值σ跟特征值类似，在矩阵Σ中也是从打到小排列，而且σ的减少特别的快。在很多情况下，前10%的甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了。也就是说，我们可以用前r大的奇异值来近似描述矩阵，因此部分奇异值分解可以如下定义：



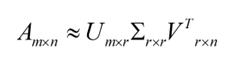
r是一个远小于m、n的数，



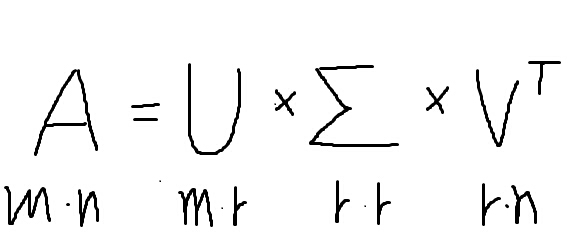
右边的三个矩阵相乘的结果将会是一个接近于A的矩阵，r越接近于n，则相乘的结果越接近于A。而这三个矩阵的面积之和要远远小于原始的矩阵A。

SVD和PCA

PCA的问题其实是一个基的变换，使得变换后的数据有着最大的方差。方差的大小描述的是一个变量的信息量，我们在讲一个东西的稳定性的时候，往往说要减小方差，如果一个模型的方差很大，那就说明模型不稳定了。但是对于机器学习的数据，方差大反而有意义，不然输入的数据就是同一个点了，那方差九尾0了。



这个假设是一个摄像机采集一个物体运动得到的图片，上面的点表示物体运动的位置，假设我们想用一条直线去拟合这些点，那我们应该选择什么方向的线？当然是图上标有signal的那条线。如果我们把这些点单纯的投影到x轴或者y轴上，最后在x轴和y轴上得到的方差就是相似的。

一般来说方差大的方向就是信号的方向，方差小的方向就是噪声的方向，我们在数据挖掘或者数字信号处理中，往往是要提高信噪比。就上图说，如果我们只保留signal方向的数据，就可以对原始数据进行不错的近似了。

PCA的就是对原始的空间中顺序地找一组相互正教的坐标轴，第一个轴使得方差最大，第二个轴是在与第一个轴相交的平面中使得方差最大，第三个轴也是在与第1,2个轴正交的平面中使得方差最大，这种假设在N维空间中，我们就可以找到N个这样的坐标轴，我们取前r个去近似这个空间，这样就从一个N维的空间压缩到r维的空间，但是我们可以选择r个坐标轴使得空间的压缩使得数据的损失最小。

假设我们矩阵的每一行代表一个样本，每一列代表一个feature，将一个m*n的矩阵A进行坐标轴的变化，P就是一个变换的矩阵从一个n维的空间变换到另外一个n维的空间





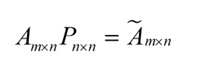
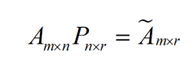
而将一个m*n的矩阵A变成一个m*r的矩阵，我们就会使得本来有n个feature的，变成有r个feature了(r小于n)，这r个其实就是对n个feature的一种提炼，我们把这个称为feature的压缩：

之前的SVD的式子是：



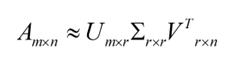
在矩阵的两边同时乘上一个矩阵V，由于v是一个正交的矩阵



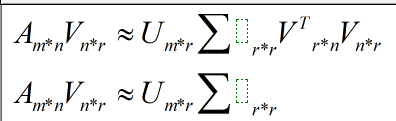
我们对SVD分解的式子两边乘以U的转置矩阵U’



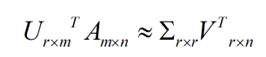
PCA几乎可以说是对SVD的一种包装，如果我们实现了SVD，那也就实现了PCA。