POJ3585 Accumulation Degree【换根dp】

题目传送门

题意

给出一棵树，树上的边都有容量，在树上任意选一个点作为根，使得往外流（到叶节点，叶节点可以接受无限多的流量）的流量最大。

分析

首先，还是从1号点工具人开始$dfs$，可以求出$dp[i]$为点$i$向它的子树中可以获得的最大流量。

接下来考虑换根，设$f[i]$是以$i$为根节点的答案（向它的所有根节点能够发射的最大流量之和）

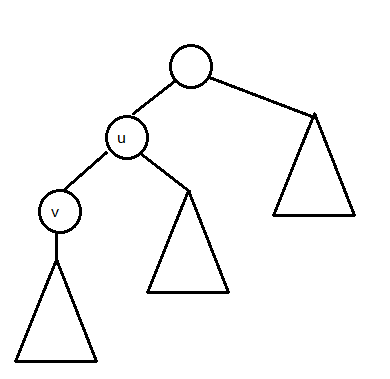
考虑把根从$u$换到$v$，$v$自己子树内的答案$dp[v]$肯定是在$f[v]$之内的

经过了$u-v$这条边的答案就是$min(f[u]-min(w,dp[v]),w)$

加起来就是$f[v]=dp[v]+min(f[u]-min(w,dp[v]),w)$

理解一下：$f[u]-min(w,dp[v])$是减去红圈里的贡献，也就是$u$不往$v$里面流也产生的答案。要取$min(w,dp[v])$是因为$u$真正能流进$v$子树里的流量还要受到$w$的限制

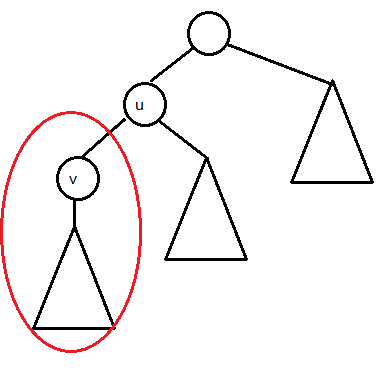
相同地，把$v$当做根之后往$u$方向流的流量也会受到$w$的限制，所以也要取$min$。

另外，特别地，还有这种情况：

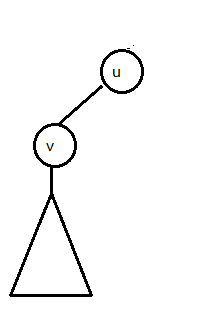
（这种情况真的好难想到的说）

这种情况的话，答案就直接是$f[v]=dp[v]+w$

然而用上面的式子的话，$f[u]-min(w,dp[v])=0$，变成$f[v]=dp[v]$，是不成立的。所以需要特判一下。

然后就做

 #include<cstdio>
 #include<algorithm>
 #include<vector>
 #include<cstring>
 using namespace std;
 #define N 200005
 #define ll long long
 #define INF 0x3f3f3f3f
 int n,ans;
 int dp[N],f[N];
 vector<pair<int,int> >G[N];
 int rd()
 {
     int f=,x=;char c=getchar();
     while(c<''||c>''){if(c=='-')f=-; c=getchar();}
     while(c>=''&&c<=''){x=(x<<)+(x<<)+(c^);c=getchar();}
     return f*x;
 }
 void dfs(int u,int p)
 {
     int tmp=;
     for(int i=;i<G[u].size();i++)
     {
         int v=G[u][i].first,w=G[u][i].second;
         if(v==p) continue;
         dfs(v,u);
         tmp+=min(dp[v],w);
     }
     if(tmp) dp[u]=tmp;
     return ;
 }
 void dfs2(int u,int p)
 {
     ans=max(ans,f[u]);
     for(int i=;i<G[u].size();i++)
     {
         int v=G[u][i].first,w=G[u][i].second;
         if(v==p) continue;
         if(G[u].size()==)
         {
             f[v]=dp[v]+w;
             dfs2(v,u);
         }
         else
         {
             f[v]=dp[v]+min(w,f[u]-min(w,dp[v]));
             dfs2(v,u);
         }
     }
 }
 int main()
 {
     int T=rd();
     while(T--)
     {
         n=rd();
         if(n==)
         {//特判
             puts("");
             continue;
         }
         ans=;
         memset(dp,INF,sizeof(dp));
         for(int i=;i<=n;i++)
             G[i].clear();
         for(int i=;i<n;i++)
         {
             int u=rd(),v=rd(),w=rd();
             G[u].push_back(make_pair(v,w));
             G[v].push_back(make_pair(u,w));
         }
         dfs(,-);
         for(int i=;i<=n;i++)
             if(dp[i]==INF)
                 dp[i]=;//叶节点
         f[]=dp[];
         dfs2(,-);
         printf("%d\n",ans);
     }
 }

Code

完啦。