HDU 6305.RMQ Similar Sequence-笛卡尔树+数学期望 (2018 Multi-University Training Contest 1 1008)

6305.RMQ Similar Sequence

这个题的意思就是对于A，B两个序列，任意的l，r，如果RMQ(A，l，r)=RMQ(B，l，r)，B序列里的数为[0,1]的实数，B的重量为B的所有元素的和，否则为0。问你B的期望重量是多少。

dls讲题说是笛卡尔树，笛卡尔树是一种特定的二叉树数据结构，具体的看这篇博客吧：【pushing my way】笛卡尔树

这个题就是笛卡尔树同构的问题，假设A的笛卡尔树的子树大小为sz[u]，那么序列B与A同构的概率为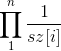，因为B中的数满足均匀分布(因为B中的元素为[0,1]中的任意实数)，所以每个位置的期望值为(0+1)/2，那么B的重量总和为n/2，所以B的重量的期望值为。

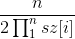贴一下官方题解:

RMQ-Similar实际上就是A和B的笛卡尔树一样，这样我们就有了一个二叉树，然后可以在树上分析了。 考虑到B中有元素相同的概率是0，于是可以假设B里面元素互不相同，也就是说可以假定是一个排列。 显然，符合笛卡尔树的排列就是这个树的拓扑序列个数，就是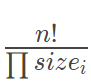。然后显然每个排列期望的和是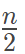，于是答案就是。

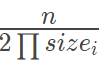代码(参考别人的模板)：

 //1008-6305-RMQ的概念、笛卡尔树模板题，同构求bi的拓扑序个数
 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<cmath>
 #include<cstdlib>
 #include<cassert>
 #include<queue>
 #include<vector>
 #include<stack>
 using namespace std;
 typedef long long ll;
 const int maxn=1e6+;
 const int inf=0x3f3f3f3f;
 const int mod=1e9+;

 stack<int>st;
 ll inv[maxn];
 int n;

 struct node{
     int val,sz;
     int l,r,par;
 }t[maxn];

 void init()
 {
     for(int i=;i<=n;i++)
         t[i].l=,t[i].r=,t[i].par=,t[i].sz=;//初始化
     t[].val=inf;
     while(!st.empty())
         st.pop();
     st.push();
 }

 void build()
 {
     for(int i=;i<=n;i++){
         while(!st.empty()&&t[st.top()].val<t[i].val)//从栈顶往栈底遍历，
             st.pop();
         int par=st.top();
         t[i].par=par;//i.par为st.pop()
         t[i].l=t[par].r;
         t[t[par].r].par=i;
         t[par].r=i;//右子树
         st.push(i);
     }
 }

 void dfs(int u)
 {
     if(u==) return ;
     t[u].sz=;
     dfs(t[u].l);
     dfs(t[u].r);
     t[u].sz+=t[t[u].l].sz+t[t[u].r].sz;
 }

 void Inv(){//扩展gcd求逆元
     inv[]=;
     for(int i=;i<maxn;i++)
         inv[i]=inv[mod%i]*(mod-mod/i)%mod;
 }

 int main()
 {
     int T;
     Inv();
     scanf("%d",&T);
     while(T--){
         scanf("%d",&n);
         init();
         for(int i=;i<=n;i++)
             scanf("%d",&t[i].val);
         build();
         dfs(t[].r);

         ll ans=n*inv[]%mod;
         for(int i=;i<=n;i++)
             ans=ans*inv[t[i].sz]%mod;
         printf("%lld\n",ans);
     }
 }

代码(标程)：

 #include <cstdio>
 #include <functional>
 #include <algorithm>
 #include <vector>
 #include <queue>

 using int64 = long long;

 const int mod = 1e9 + ;

 int main() {
   int T;
   scanf("%d", &T);
   for (int cas = ; cas <= T; ++cas) {
     int n;
     scanf("%d", &n);
     std::vector<int> a(n);
     for (int i = ; i < n; ++i) {
       scanf("%d", &a[i]);
     }

     std::vector<int> left(n, -), right(n, -), stk(n), parent(n, -);
     for (int i = , top = ; i < n; ++i) {
       int last = -;
       while (top && a[i] > a[stk[top - ]]) {
         last = stk[--top];
       }
       if (top) {
         right[stk[top - ]] = i;
         parent[i] = stk[top - ];
       }
       left[i] = last;
       if (last != -) parent[last] = i;
       stk[top++] = i;
     }

     std::vector<int> inv(n + , );
     for (int i = ; i < n + ; ++i) {
       inv[i] = int64(mod - mod / i) * inv[mod % i] % mod;
     }

     using pii = std::pair<int, int>;
     {
       std::vector<pii> a(n), b(n);
       std::queue<int> queue;
       std::vector<int> cnt(n);
       for (int i = ; i < n; ++i) {
         a[i] = b[i] = {inv[], };
         if (left[i] == - && right[i] == -) {
           queue.push(i);
         }
         cnt[i] = (left[i] != -) + (right[i] != -);
       }
       while (!queue.empty()) {
         int u = queue.front(); queue.pop();
         pii res = {(int64)a[u].first * inv[a[u].second] % mod * b[u].first % mod * inv[b[u].second] *  % mod, a[u].second + b[u].second + };
         int p = parent[u];
         if (p == -) {
           printf("%d\n", res.first);
           break;
         }
         if (cnt[p] == ) a[p] = res;
         else if (cnt[p] == ) b[p] = res;
         --cnt[p];
         if (cnt[p] == ) queue.push(p);
       }
     }
   }
   return ;
 }

讲道理，还是有点不太清楚，还不熟练，多学习一下。

溜了。。。