斯坦福机器学习视频笔记 Week2 多元线性回归 Linear Regression with Multiple Variables

相比于week1中讨论的单变量的线性回归，多元线性回归更具有一般性，应用范围也更大，更贴近实际。

Multiple Features

上面就是接上次的例子，将房价预测问题进行扩充，添加多个特征（features），使问题变成多元线性回归问题。

多元线性回归将通过更多的输入特征，来预测输出。上面有新的Notation（标记）需要掌握。

相比于之前的假设：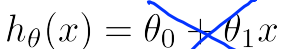

我们将多元线性回归的假设修改为：

每一个xi代表一个特征；为了表达方便，令x0=1，可以得到假设的矩阵形式：

其中，x和theta分别表示：

所有的训练样本按行存贮在矩阵X中，看一个例子：

这样，我们可以通过向量的计算，直接得到一个m×1的假设结果向量：

Gradient Descent For Multiple Variables

梯度下降的通用形式依然不会变化：

只是，和单变量线性回归不同的是，多元线性回归需要同时迭代n+1个theta；

Gradient Descent in Practice I - Feature Scaling

特征归一化，总的说来是为了让特征之间的数值差距缩小，使数据分散在同一个数量级范围。

关于这样做的好处，可以减小数量级偏大的特征对数量级偏小特征的影响，比如上面所说的房屋面积size，和卧室数量；

如果将这两个特征画在上面的二维图中，就会变成一个瘦长的椭圆。

总之，如果想要使梯度下降算法收敛的更快，就需要使用特征归一化Feature Scaling，使特征分布在相近的范围中。

使新的特征最好分布在[-1,1]中，如上面使用xi/（数据范围：max-min）。

通常情况下，数据分布在[-1/3,1/3] or [-3,3]都是可以接受的。

正规化均值，使数据集的均值为0.（不要对x0使用）

可以一步同时完成数据归一和正规化：

其中μi为对应特征的均值；Si是特征数据已知的分布范围，通常是（max - min）来计算，或者为数据的标准差。

Gradient Descent in Practice II - Learning Rate

学习率a对于梯度下降是关键，下面就来讨论如何选取使算法高效运行的a值。

我们可以作关于损失函数 J（theta）和 迭代次数的函数，在指定的学习率a下的图象，

如果函数 J 不是单调减小的，那么需要减小a。

多次选择a，需要得到一个足够小的a，使得 J 在每一步迭代中都 不断减小；

但是如果a太小，梯度下降会收敛的很慢，这时也需要略微增大a。

选择a的原则：最好先找到最大的使 J 单调减小的a，最终选择比最大的a略小的值。

每次选择可以增大或减小3倍，然后再增大或减小数量级。

Features and Polynomial Regression

实际应用中，我们只使用简单的‘直线’回归显然是不够的，我们大多数情况下需要使用多项式拟合。

单看这些数据点的分布，直观上感觉使用曲线比直线拟合的效果要好一些。

根据实际的例子，关于房价的预测，size越大，房价不会下跌，选用三次函数拟合数据更好。

同时，平方根函数也是不错的选择：。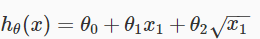

（注：如使用多项式回归，一定要使用特征归一化）

Normal Equation

Normal Equation是另外一种求参数theta的方法。

我们知道，梯度下降反复迭代的目的，就是求得那个最优解，而Normal Equation的思想就是直接通过求导，得到theta。

其对所有的θj分别求偏导数，然后使它们为0，解这些方程组，求得theta。

这样就不需要通过反复迭代而直接求得结果，效率颇高。下面是一个例子：

这是方法的矩阵表示：

相较于梯度下降，Normal Equation有以下优势：

不需要选择a，不需要进行迭代，只需计算一个n×n的转置矩阵，算法效率高，

而且在Normal Equation中不需要进行特征归一化操作。

注意：当n>10,000时，Normal Equation的计算代价过大，建议使用梯度下降。

Normal Equation Noninvertibility

如果X^TX不可逆，根据上面的Normal Equation求theta的公式，原则上是不能使用的，那应该怎么处理这种情况？

X^TX不可逆的情况：

1）冗余的特征（呈线性关系）：删除多余的特征；

2）特征过多，训练数据过少(m<=n)：删除某些特征，或 使用“regularization ”。