【bzoj 4407】于神之怒加强版

Description

给下N,M,K.求

 

 

Input

输入有多组数据，输入数据的第一行两个正整数T,K，代表有T组数据，K的意义如上所示，下面第二行到第T+1行，每行为两个正整数N,M，其意义如上式所示。

Output

如题

Sample Input

1 2
3 3

Sample Output

20

HINT

1<=N,M,K<=5000000,1<=T<=2000

题解：

（若因博客园导致数学公式重叠，建议Ctrl+滑轮，重新缩放）

$ans=\sum_{i=1}^{n}\sum_{j=1}^{m}\gcd(i,j)^{k}$

$=\sum_{d=1}^{n}d^{k}\sum_{i=1}^{\lfloor \frac{n}{d} \rfloor}\sum_{j=1}^{\lfloor \frac{m}{d} \rfloor}[\gcd(i,j)==1]$

$=\sum_{d=1}^{n} d^{k}\sum_{k=1}^{\lfloor \frac{n}{d} \rfloor}\mu(k)\lfloor\frac{n}{kd}\rfloor\lfloor\frac{m}{kd}\rfloor$

$=\sum_{T=1}^{n}\lfloor \frac{n}{T}\rfloor\lfloor \frac{m}{T}\rfloor\sum_{d|T}\mu(\frac{T}{d})d^{k}$

再设：$g(T)=\sum_{d|T}\mu(\frac{T}{d})d^{k}$

当T是质数时

$g(T)=T^{k}\mu(1)+1^{k}\mu(T)=T^{k}-1$

当i与p互质时

对于$g（i）$约数的每个枚举其内部多了$g(p)$的约数枚举

$\therefore g(i*p)=g(i)*g(p)$

当i与p不互质时

首先$i=p^{x}*t$

由莫比乌斯函数定义可知，对g(i)存在贡献的d中至少含有x-1个p

因此在$g(i*p)$的枚举中，每个数值d（i*p）都对应着$g(i)$中的一个枚举数值d（i）满足：
$d(i*p)=d(i)*p$

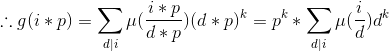
$                 =g(i)*p^{k} $

然后分块+线筛即可