------ 新春第一炮：阶乘算法性能分析与 double fault 蓝屏故障排查 Part I ------

——————————————————————————————————————————————————————————————————————————

春节期间闲来无事想研究下算法，上机测试代码却遇到了意外错误，在此记录整个过程，祝各位新的一年在算法设计和故障排查方面的思维敏锐度媲美 dog 的

嗅觉！

——————————————————————————————————————————————————————————————————————————

整数 n 的阶乘（factorial）记作“n!”，比如要计算 5!，那么就是计算 5 * 4 * 3 * 2 * 1 = 120。

在 32 位系统上，“unsigned int（ULONG）”型变量能够持有的最大 10 进制值为 4,294,967,295（FFFF FFFF），意味着无符号数最多只能用来计算

12!（479,001,600 = 1C8C FC00）；若计算 13!（6,227,020,800 = 1 7328 CC00）就会发生溢出。

类似地，“int”型变量能够持有的最大 10 进制值为 2,147,483,647（7FFF FFFF），意味着有符号数最多也只能用来计算

12!；若计算 13! 就会发生下溢（8000 0000 = -2,147,483,648）。

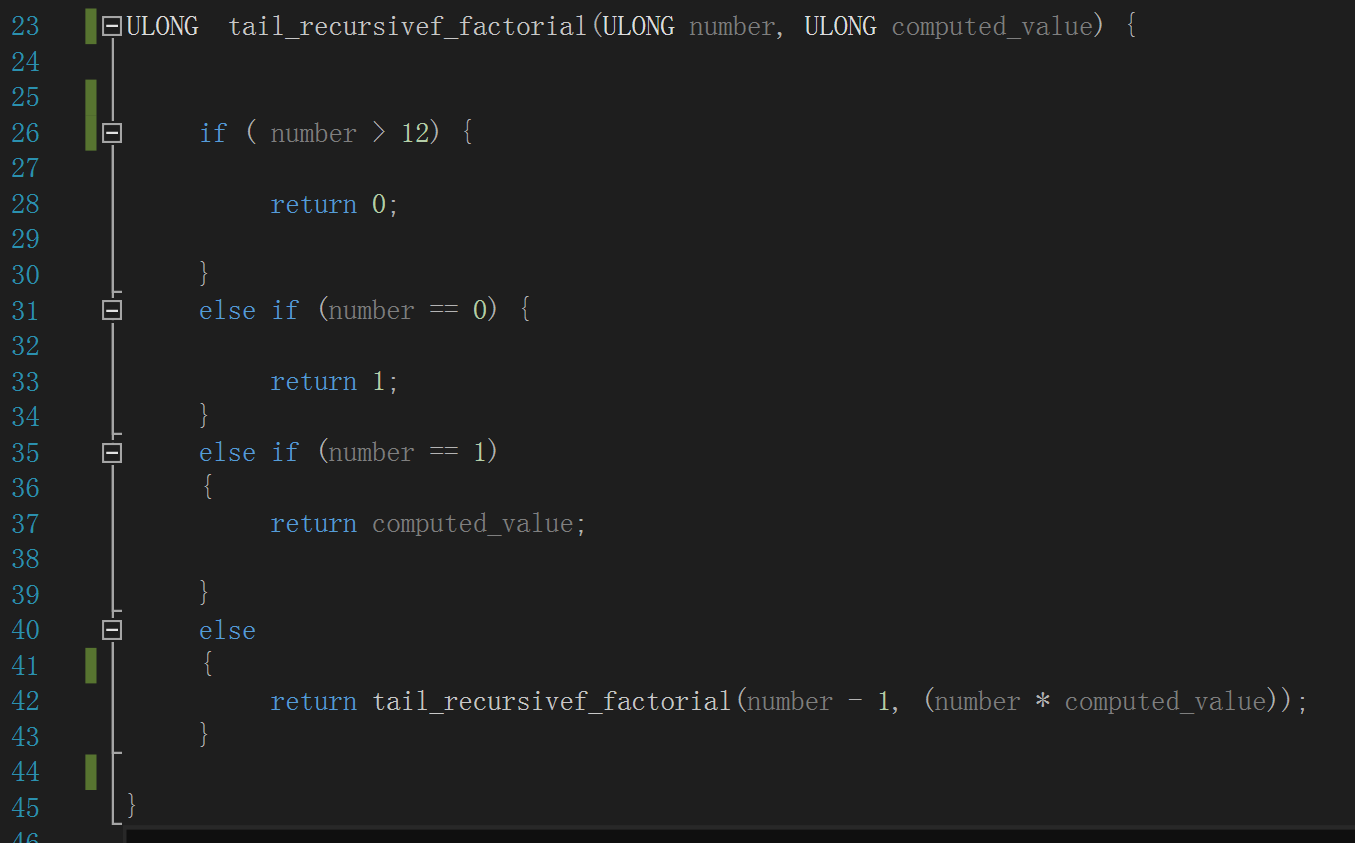
一般的编程范式通常以函数递归调用自身来实现阶乘计算，并在函数内部添加递归的终止条件。

下图是一种叫做“尾递归”的阶乘计算算法，从源码级别来看，它的巧妙之处在于第二个形参“computed_value”可以用来保存

本次递归的计算结果，然后作为下一次的输入。每次第一个参数“number”的值都递减，终止条件就是当它降到 1 时，即返回最新的 computed_value

值。“tail_recursivef_factorial()”开头的判断逻辑确保了我们不会因为计算 13! 或更大数的阶乘导致溢出：

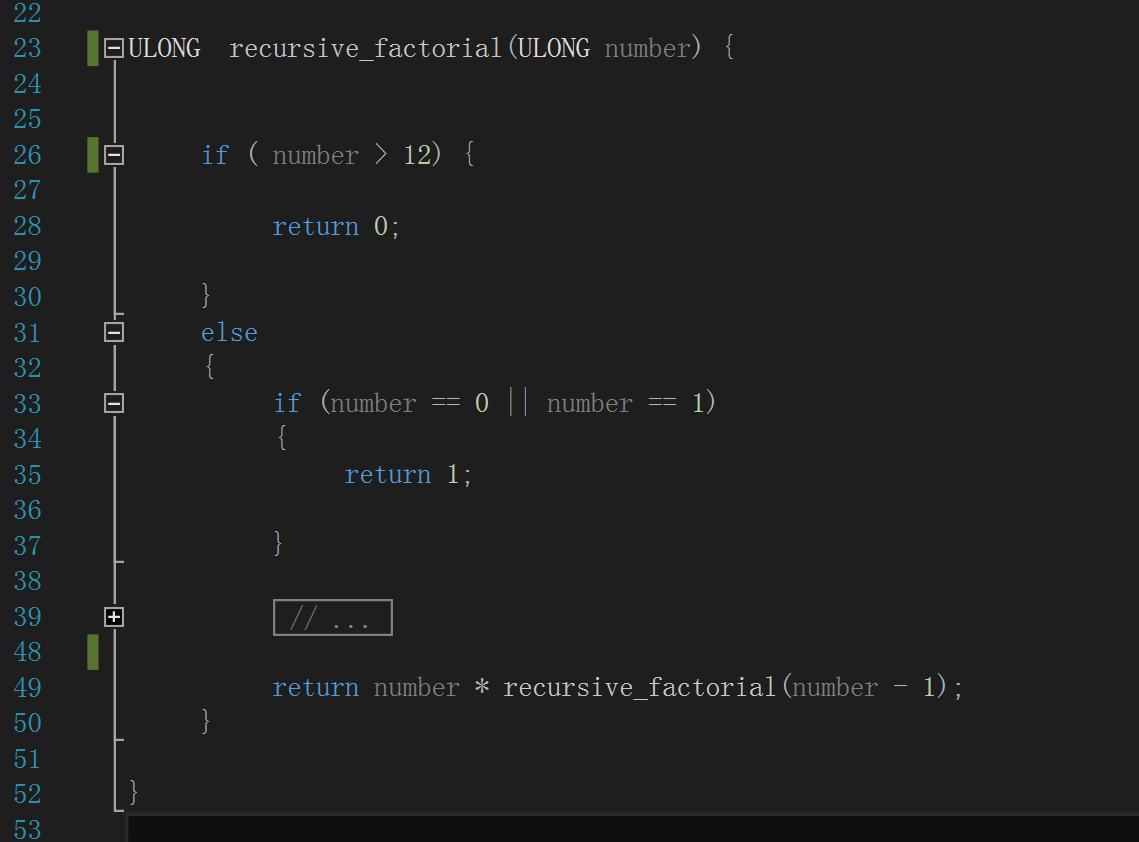
作为对比，下图则是另一种“基本递归”的阶乘计算算法，“recursive_factorial()”只有一个形参，就是要计算阶乘的正整数。

前面的逻辑大致与 tail_recursivef_factorial() 相同，除了最后那条 return 语句，它把对自身的递归调用放进了一个表达式中，这种做法对性能的影响是

致命的，因为不得不等待递归调用终止才能完成整个表达式的求值计算：

————————————————————————————————————————————————————————————————————————————————————

假设我们忽略溢出的情况，或者在 64 位系统上执行这段代码，就可以传入更大的正整数。而从源码上看，recursive_factorial() 的性能严重依赖于输入

参数——试想要计算 100!，它可能需要反复地创建，销毁函数调用栈帧 100 次，才能完成表达式求值并返回。

反观 tail_recursivef_factorial()，因为它引入了一个额外变量存储每次调用的结果，从形式上而言与 for 循环并无太大区别，

“貌似”编译器可以优化这段代码来生成与 for 循环类似的汇编指令，从而避免函数调用造成的额外 CPU 时钟周期开销（反复的压栈弹栈都需要访问内

存）。

我们的美好愿望是：同样计算 100!，tail_recursivef_factorial() 无需多余的 99 次函数调用栈帧开销，在汇编级别直接用与类似 for 循环的迭代控制结构即可

实现相同效果，使得执行时间大幅缩短。

在后面的调试环节你会看到：这个“美好愿望”或许对其它编译器而言能够成立，对 Visual C/C++ 编译器而言则不行——它还不够智能来进行尾递归优化

（或称尾递归“消除”）。

做性能分析就需要计算两者的执行时间，我们使用内核例程“KeQuerySystemTime()”，分别在两个函数各自的调用前后获取一次当前系统时间，然后相减

得出差值，它就是两种阶乘计算算法的运行时间，如下图，注意黄框部分的逻辑，变量“execution_time_of_factorial_algorithm”存储它们各自的运行时

间：

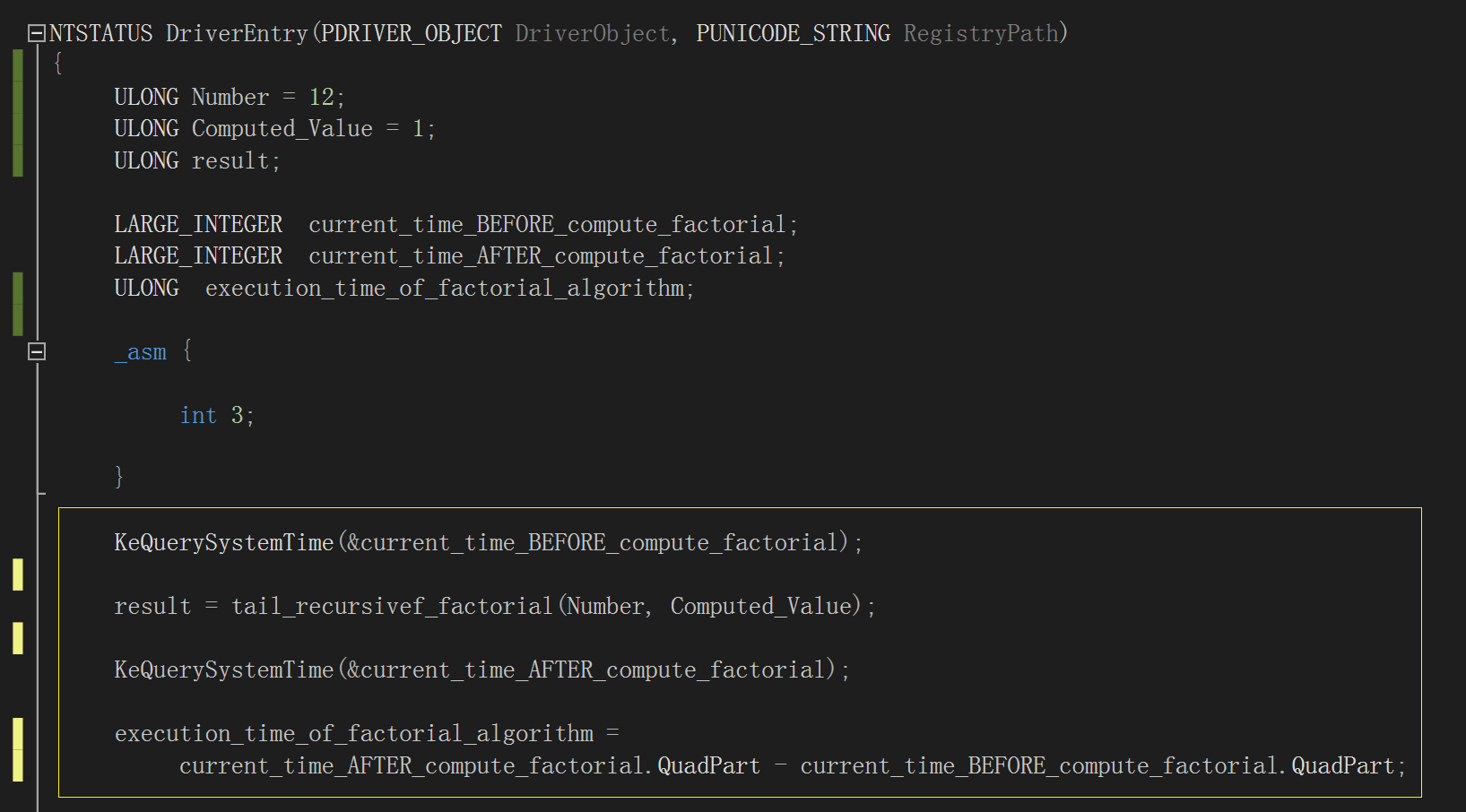
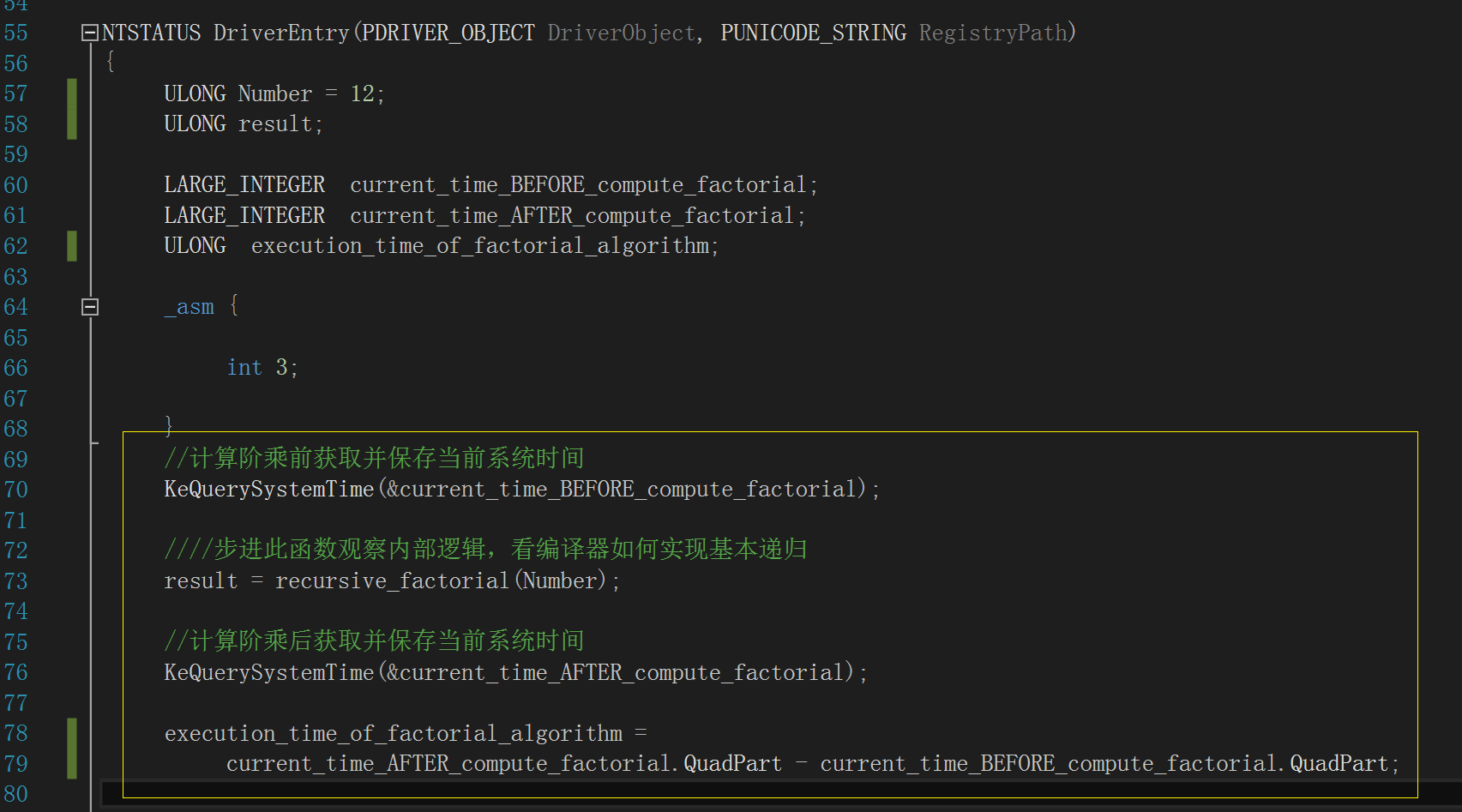
图中以内联汇编添加的软件断点是为了方便观察 KeQuerySystemTime() 如何使用“LARGE_INTEGER”这个结构体：

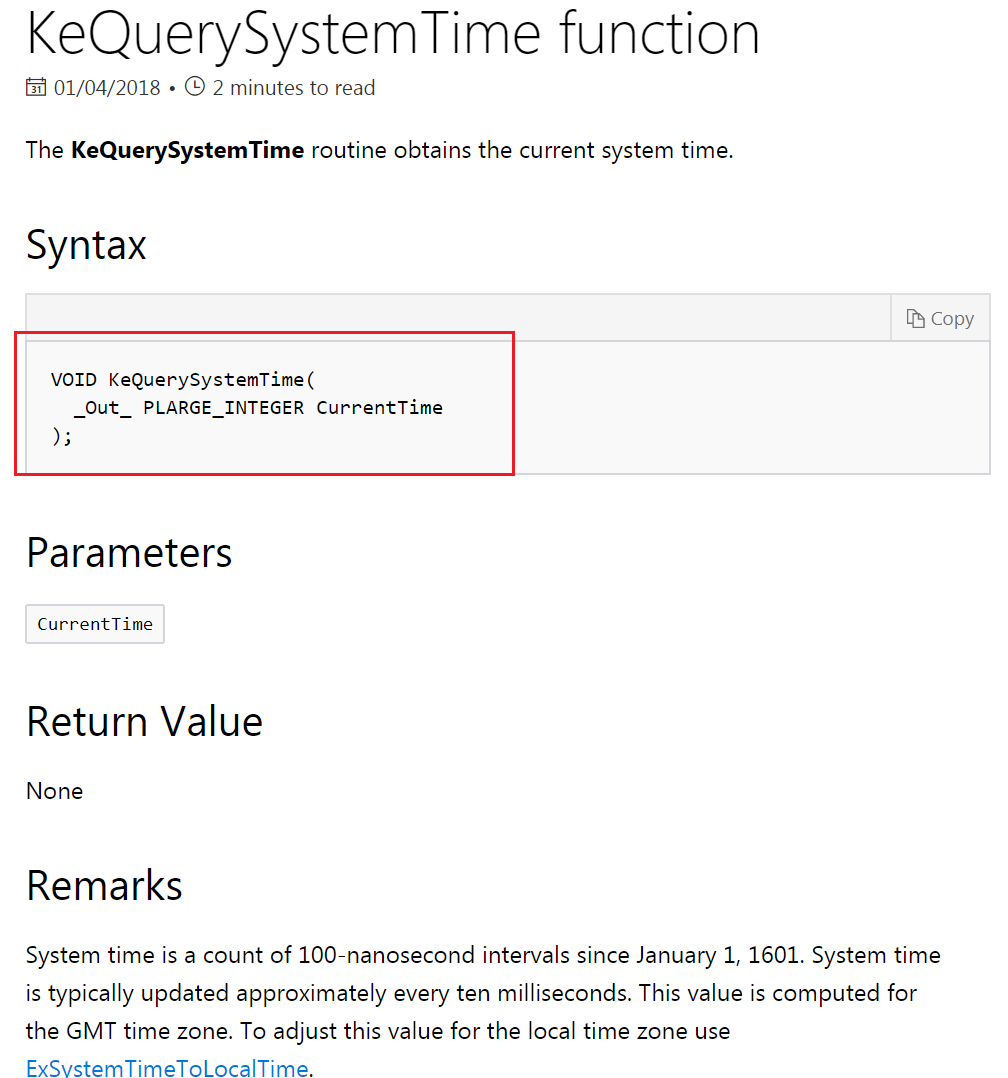
原始文档写得很清楚—— KeQuerySystemTime() 输出的系统时间（由一枚“LARGE_INTEGER”型指针引用）

是从 1601年1月1日开始至当前的“100 纳秒”数量，通常约每 10 毫秒会更新一次系统时间。

KeQuerySystemTime() 的输出值是根据 GMT 时区计算的，使用 ExSystemTimeToLocalTime() 可以把它调整为本地时区的值。

既然 1 毫秒 = 1000 微秒 = 1000000 纳秒，只需把这个值除以 10000 即可得到“毫秒数”，再除以 1000 即可得出以秒为单位

的运行时间。

但是事情没那么简单，你想看看：从 1601年1月1日以来到当前 KeQuerySystemTime() 调用经历了多少个“100 纳秒”，无论这个

数值为何，肯定不是 32 位系统上的 4 字节变量能够容纳得下的，所以要么在 64 位 Windows 上调试这段代码，要么必须使用

LARGE_INTEGER 结构体的 QuadPart 字段，该字段实质上是内存中一个连续的 8 字节区域：

以 32 位系统而言，ULONG 型变量最多支持 4294967295 个“100 纳秒”，亦即 429 秒；换言之，阶乘算法运行超过 7 分钟，

就无法用 ULONG 变量（execution_time_of_factorial_algorithm）存储执行时间（该值已溢出所以不正确）。