CF266D. BerDonalds [图的绝对中心]

D. BerDonalds

time limit per test

5 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

BerDonalds, a well-known fast food restaurant, is going to open a cafe in Bertown. The important thing is to choose the new restaurant's location so that it would be easy to get there. The Bertown road system is represented by n junctions, connected by m bidirectional roads. For each road we know its length. We also know that we can get from any junction to any other one, moving along the roads.

Your task is to find such location of the restaurant, that the shortest distance along the roads from the cafe to the farthest junction would be minimum. Note that the restaurant can be located not only on the junction, but at any point of any road.

Input

The first line contains two integers n and m (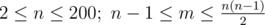) — the number of junctions and the number of roads, correspondingly. Then m lines follow, describing all Bertown roads. Each road is described by three integers ai, bi, wi(1 ≤ ai, bi ≤ n, ai ≠ bi; 1 ≤ wi ≤ 105), where ai and bi are the numbers of the junctions, connected by the i-th road, and wi is the length of the i-th road.

It is guaranteed that each road connects two distinct junctions, there is at most one road between any two junctions, and you can get from any junction to any other one.

Output

Print a single real number — the shortest distance from the optimal restaurant location to the farthest junction. The answer will be considered correct, if its absolute or relative error doesn't exceed 10 - 9.

---

比赛的时候想了一种做法；

先floyd，然后枚举每条边，在边上二分一个点使得这个点到其他点最大距离最小

但是一直WA，问题竟然是，这不是个单调函数是个单峰函数应该用三分！！！

然后貌似这个道卡三分了

二分是可以做的，直接二分答案ans，然后也是枚举每条边让其他点向这条边走ans距离，没有走到的地方覆盖，最后全覆盖了就是不可行

但是有复杂度更低的做法O(n^3)  参考http://www.cnblogs.com/lzqxh/archive/2013/03/05/2944834.html#2659117

枚举边后，对于每个点距离是min{d[u][i]+x,d[v][i]+L-x}，是单峰函数，并且是一个折，所有点画出来长这样

最优解一定在最上面那条线的最低点取到

那就找所有交点

按照d[u][]大到小排序后，对于先后两个点a和b，他们的图像出现交点的条件就是d[v][a]<d[v][b]

还有一点，这个距离最多是个0.5  (这也解释了为什么本题精度那么奇怪)

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
using namespace std;
const int N=,M=2e4+,INF=1e9+;
inline int read(){
    char c=getchar();int x=,f=;
    while(c<''||c>''){if(c=='-')f=-; c=getchar();}
    while(c>=''&&c<=''){x=x*+c-''; c=getchar();}
    return x*f;
}
 
int n,m,u,v,w;
struct data{
    int u,v,w;
}a[M];
int d[N][N];
void floyd(){
    for(int k=;k<=n;k++)
        for(int i=;i<=n;i++)
            for(int j=;j<=n;j++)
                d[i][j]=min(d[i][j],d[i][k]+d[k][j]);
}
 
int ans=INF;
int rnk[N][N],val[N];
bool cmp(int a,int b){return val[a]<val[b];}
void solve(){
    floyd();
    for(int i=;i<=n;i++){
        for(int j=;j<=n;j++) rnk[i][j]=j,val[j]=d[i][j];
        sort(rnk[i]+,rnk[i]++n,cmp);
        //for(int j=1;j<=n;j++) printf("rnk %d %d %d\n",i,j,rnk[i][j]);
    }
    for(int i=;i<=n;i++) ans=min(ans,d[i][rnk[i][n]]<<);
    for(int i=;i<=m;i++){
        u=a[i].u,v=a[i].v,w=a[i].w;
        for(int p=n,i=n-;i>=;i--){
            if(d[v][rnk[u][i]]>d[v][rnk[u][p]]){//rnk[u][i] and rnk[u][p] has intersectioin
                ans=min(ans,d[u][rnk[u][i]]+d[v][rnk[u][p]]+w);
                p=i;
            }
        }
    }
    printf("%lf",ans/2.0);
}
 
int main(){
    n=read();m=read();
    for(int i=;i<=n;i++) for(int j=i+;j<=n;j++) d[i][j]=d[j][i]=INF;
    for(int i=;i<=m;i++){
        a[i].u=read(),a[i].v=read(),a[i].w=read();
        d[a[i].u][a[i].v]=d[a[i].v][a[i].u]=a[i].w;
    }
    solve();
}