机器学习基石:07 The VC Dimension

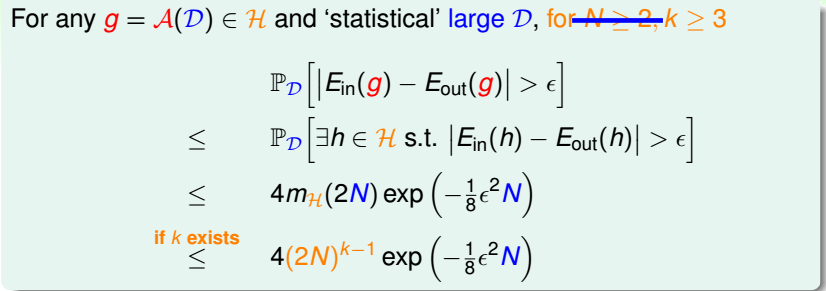












机器学习基石:07 The VC Dimension的更多相关文章
- 机器学习基石笔记:07 The VC Dimension
当N大于等于2,k大于等于3时, 易得:mH(N)被Nk-1给bound住. VC维:最小断点值-1/H能shatter的最大k值. 这里的k指的是存在k个输入能被H给shatter,不是任意k个输入 ...
- 07 The VC Dimension
当N大于等于2,k大于等于3时, 易得:mH(N)被Nk-1给bound住. VC维:最小断点值-1/H能shatter的最大k值. 这里的k指的是存在k个输入能被H给shatter,不是任意k个输入 ...
- 机器学习基石7-The VC Dimension
注: 文章中所有的图片均来自台湾大学林轩田<机器学习基石>课程. 笔记原作者:红色石头 微信公众号:AI有道 前几节课着重介绍了机器能够学习的条件并做了详细的推导和解释.机器能够学习必须满 ...
- 【The VC Dimension】林轩田机器学习基石
首先回顾上节课末尾引出来的VC Bound概念,对于机器学习来说,VC dimension理论到底有啥用. 三点: 1. 如果有Break Point证明是一个好的假设集合 2. 如果N足够大,那么E ...
- 【机器学习基石笔记】七、vc Dimension
vc demension定义: breakPoint - 1 N > vc dimension, 任意的N个,就不能任意划分 N <= vc dimension,存在N个,可以任意划分 只 ...
- Coursera台大机器学习课程笔记6 -- The VC Dimension
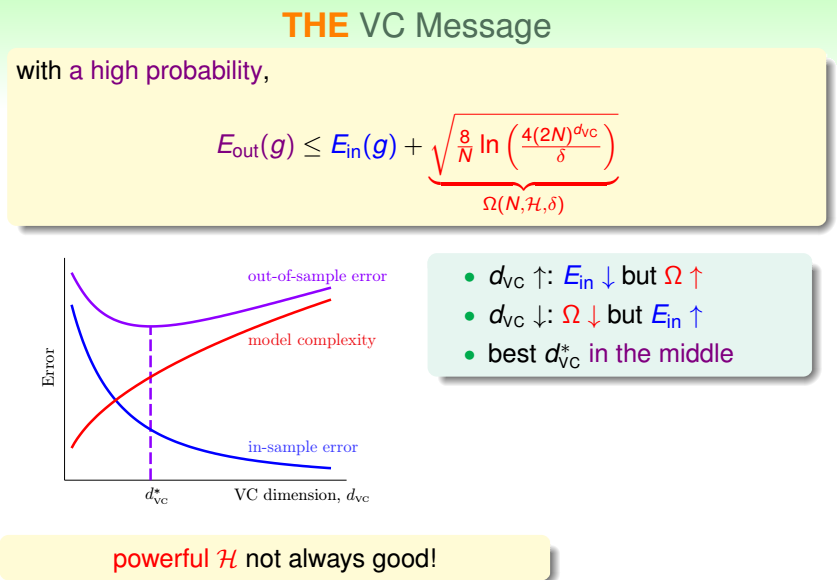
本章的思路在于揭示VC Dimension的意义,简单来说就是假设的自由度,或者假设包含的feature vector的个数(一般情况下),同时进一步说明了Dvc和,Eout,Ein以及Model C ...
- 机器学习基石12-Nonlinear Transformation
注: 文章中所有的图片均来自台湾大学林轩田<机器学习基石>课程. 笔记原作者:红色石头 微信公众号:AI有道 上一节课介绍了分类问题的三种线性模型,可以用来解决binary classif ...
- 机器学习基石8-Noise and Error
注: 文章中所有的图片均来自台湾大学林轩田<机器学习基石>课程. 笔记原作者:红色石头 微信公众号:AI有道 上一节课,我们主要介绍了VC Dimension的概念.如果Hypothese ...
- 机器学习基石11-Linear Models for Classification
注: 文章中所有的图片均来自台湾大学林轩田<机器学习基石>课程. 笔记原作者:红色石头 微信公众号:AI有道 上一节课,我们介绍了Logistic Regression问题,建立cross ...
随机推荐
- Notepad++使用vs2015主题教程
前言: 最近几天都在用Notepad++,所以想换个看得舒服点的主题. 发现vs2015的主题颜色特别好看.所以就查了一下有没有大佬做了这样的Notepad++主题. 结果是有的. 正文: notep ...
- NOIP知识点
基础算法 贪心 枚举 分治 二分 倍增 高精度 模拟 图论 图 最短路(dijkstra.spfa.floyd) 最小生成树(kruskal.prim) 并查集 拓扑排序 二分图染色 Tarjan 树 ...
- JavaScript(第二十五天)【事件绑定及深入】
事件绑定分为两种:一种是传统事件绑定(内联模型,脚本模型),一种是现代事件绑定(DOM2级模型).现代事件绑定在传统绑定上提供了更强大更方便的功能. 一.传统事件绑定的问题 传统事件绑定有内联模型 ...
- 利用jmeter做一个简单的性能测试并进行参数化设置
1.新增一个线程组,并在下面添加基本原件,包括:监听器.http请求默认值和一个事务控制器 在http请求默认值中填写 ip 地址和端口号,协议类型默认为http 2.添加代理服务器,以便之后进行录制 ...
- Session的过期时间如何计算?
在生成session的时候,会设置一个session过期时间.session的过期时间并不是从生成session对象开始计算,超过过期时间,session就失效了. 而是每当一个浏览器请求,sessi ...
- vue初尝试--项目结构
新建一个项目之后,我们来看一下项目的目录结构 几个主要文件的内容 index.html文件(入口文件,系统进入之后先进入index.html) <!DOCTYPE html> <ht ...
- Web Api 返回图片流
public class TestController : ApiController { public HttpResponseMessage GetImg() { //获取文件的绝对路径 stri ...
- 回收 PV - 每天5分钟玩转 Docker 容器技术(152)
当 PV 不再需要时,可通过删除 PVC 回收. 当 PVC mypvc1 被删除后,我们发现 Kubernetes 启动了一个新 Pod recycler-for-mypv1,这个 Pod 的作用就 ...
- tomcat 修改默认字符集
找到connector节点,插入 disableUploadTimeout="true" useBodyEncodingForURI="true" URIEnc ...
- 证明二叉查找树所有节点的平均深度为O(logN)
数据结构与算法分析(c语言描述)第4章 P78 概念一:一棵树所有节点的深度和称为内部路径长 令D(N)为一棵有N节点的树的内部路径长么,即有D(1)=0, 设一棵树的左子树的内部路径长为D(i),则 ...
