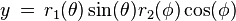d3可视化实战03：神奇的superformula

需求驱动实现

前文讲过了D3的数据驱动机制，中间所举的例子都很简单。例如那个demo里面，绑定的数据是一个简单的数组，实现的图元也仅仅是一堆用SVG画的circle。但是现实世界中我们往往会遇到复杂的需求，例如我就遇到了这样一个需求：数据是一个复杂的对象数组，而与之绑定的图元是一个可变图形。该图形可以根据与他绑定的数据中的具体参数，在圆形、方块、三角之间切换，并且要求过渡自然。

面对这个需求，最直接的做法是把圆形、方块、三角用SVG的<circle>圆形标签，<rect>矩形标签以及<polygon>多边形标签来分别实现。具体用D3实现，就是创建一个<g>集合标签作为数据绑定对象，根据数据参数的变化，remove里面的原有图形，add新的图形，从而实现数据驱动的图形更新。但是这种方法有一个很难解决的问题，就是图形切换时的过渡动画很难平滑。因为每个图形都是独立的标签，除了采用淡入淡出之类的过渡方法外，很难想到有什么更好的过渡效果。并且出于对代码简化的考虑，g标签内包裹其他的图形标签的方式，也增加了复杂度。

那么还有其他方案吗？如果能有一个万能图形标签来来实现各种图形，把数据直接绑定给它，那就再好不过了。事实上SVG的<path>路径标签就可以实现这一点。在我之前的文章”d3可视化实战01：理解SVG元素特性“中已经提到，路径功能非常强大几乎可以描绘任何图形。唯一的问题是，如何指定Path的具体参数。对于一般情况，我们可以自己设定参数。而在这里，我打算用一个数学模型来指定path的具体参数，那就是superfomula超级方程式。最终实现的效果果然非常好，动画过渡非常平滑，图元本身也很简单。下面让我们看看这个superfomula究竟是何方神圣吧。

about超级方程式

我们知道，很多数学函数都可以用解析式的方式表示，亦可根据变量和自变量的值在不同坐标系下绘成各种图形。Johan Gielis博士提出了一个函数，可以描述自然界中发现的众多复杂图形和曲线，它就是超级方程式superfomula。

超级方式的解析式如下：

在极坐标系下，r代表半径，代表角度，a,b,m,n1,n2,n3是可变参数。通过调整参数的值，就可以绘出各种图形。下图展示了a=b=1的情况下，m,n1,n2,n3取不同值的时候superfomula所展示的图形：

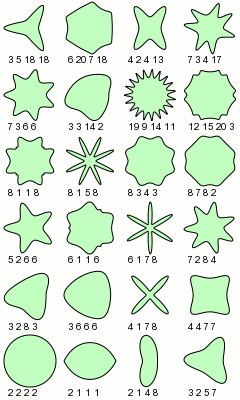
只通过控制这些参数，就能在极坐标系下绘制如此不同的各种2D图形，是不是很神奇？这就是数学这一自然科学的王冠学科的魅力。

关于superfomula的更多介绍：

superfomula的发表者Johan Gielis博士（1962-）原本的研究方向是园艺工程和生物学。在他的早期研究阶段他就感兴趣于使用数学模型表征生物生长性状。1994年发表的论文中他就开始开始使用曲线描述自然形状，在1997年的论文中他发现广义的曲线模型适用于任何对称形状。在2003年发表于美国植物学杂志上的论文A generic geometric transformation that unifies a large range of natural and abstract shapes中，他提出了superfomula。superfomula是超级椭圆公式superellipse的扩展，但具有更广泛的实用性。此后数百篇论文都引用了superfomula，并且以superfomula为指导的计算机绘图程序也随之出现。2004年johan Gielis博士收到了InterTech技术创新卓越奖，该奖主要颁发给对平面艺术及相关产业产生重大影响的技术发明。superfomula从生物技术研究中诞生，在数学领域中升华，并最终应用到计算机、平面设计等领域。可谓是跨学科研究应用的最好案例之一。

superfomula也可以扩展到3维，4维甚至更多维度。例如3维情况下，图形可以通过两个superfomula r1, r2来生成。其极坐标系与笛卡尔坐标系之间转换关系为：

其中，变量值域为[ -π/2 , π/2] (latitude维度)， θ变量值域为 [ -π, π] (longitude精度).

案例及代码实现

在github上，已经有人用D3实现了基于superfomula的图形绘制程序。大家请点击这里：http://bl.ocks.org/mbostock/1021103. 该程序的关键是基于D3的superfomula开源插件。本着学习的目的，这里保存了该插件的源码，你可以复制它然后保存为d3-superfomula.js来使用：

(function() {

var _symbol = d3.svg.symbol(),

_line = d3.svg.line();

d3.superformula = function() {

var type = _symbol.type(),

size = _symbol.size(),

segments = size,

params = {};

function superformula(d, i) {

var n, p = _superformulaTypes[type.call(this, d, i)];

for (n in params) p[n] = params[n].call(this, d, i);

return _superformulaPath(p, segments.call(this, d, i), Math.sqrt(size.call(this, d, i)));

}

superformula.type = function(x) {

if (!arguments.length) return type;

type = d3.functor(x);

return superformula;

};

superformula.param = function(name, value) {

if (arguments.length < 2) return params[name];

params[name] = d3.functor(value);

return superformula;

};

// size of superformula in square pixels

superformula.size = function(x) {

if (!arguments.length) return size;

size = d3.functor(x);

return superformula;

};

// number of discrete line segments

superformula.segments = function(x) {

if (!arguments.length) return segments;

segments = d3.functor(x);

return superformula;

};

return superformula;

};

function _superformulaPath(params, n, diameter) {

var i = -1,

dt = 2 * Math.PI / n,

r = 0,

points = [];

while (++i < n) {

t = params.m * (i * dt - Math.PI) / 4;

t = Math.pow(Math.abs(Math.pow(Math.abs(Math.cos(t) / params.a), params.n2)

+ Math.pow(Math.abs(Math.sin(t) / params.b), params.n3)), -1 / params.n1);

if (t > r) r = t;

points.push(t);

}

r = diameter * Math.SQRT1_2 / r;

i = -1; while (++i < n) {

x = (t = points[i] * r) * Math.cos(i * dt);

y = t * Math.sin(i * dt);

points[i] = [Math.abs(x) < 1e-6 ? 0 : x, Math.abs(y) < 1e-6 ? 0 : y];

}

return _line(points) + "Z";

}

var _superformulaTypes = {

asterisk: {m: 12, n1: .3, n2: 0, n3: 10, a: 1, b: 1},

bean: {m: 2, n1: 1, n2: 4, n3: 8, a: 1, b: 1},

butterfly: {m: 3, n1: 1, n2: 6, n3: 2, a: .6, b: 1},

circle: {m: 4, n1: 2, n2: 2, n3: 2, a: 1, b: 1},

clover: {m: 6, n1: .3, n2: 0, n3: 10, a: 1, b: 1},

cloverFour: {m: 8, n1: 10, n2: -1, n3: -8, a: 1, b: 1},

cross: {m: 8, n1: 1.3, n2: .01, n3: 8, a: 1, b: 1},

diamond: {m: 4, n1: 1, n2: 1, n3: 1, a: 1, b: 1},

drop: {m: 1, n1: .5, n2: .5, n3: .5, a: 1, b: 1},

ellipse: {m: 4, n1: 2, n2: 2, n3: 2, a: 9, b: 6},

gear: {m: 19, n1: 100, n2: 50, n3: 50, a: 1, b: 1},

heart: {m: 1, n1: .8, n2: 1, n3: -8, a: 1, b: .18},

heptagon: {m: 7, n1: 1000, n2: 400, n3: 400, a: 1, b: 1},

hexagon: {m: 6, n1: 1000, n2: 400, n3: 400, a: 1, b: 1},

malteseCross: {m: 8, n1: .9, n2: .1, n3: 100, a: 1, b: 1},

pentagon: {m: 5, n1: 1000, n2: 600, n3: 600, a: 1, b: 1},

rectangle: {m: 4, n1: 100, n2: 100, n3: 100, a: 2, b: 1},

roundedStar: {m: 5, n1: 2, n2: 7, n3: 7, a: 1, b: 1},

square: {m: 4, n1: 100, n2: 100, n3: 100, a: 1, b: 1},

star: {m: 5, n1: 30, n2: 100, n3: 100, a: 1, b: 1},

triangle: {m: 3, n1: 100, n2: 200, n3: 200, a: 1, b: 1}

};

d3.superformulaTypes = d3.keys(_superformulaTypes);

})();