bzoj3202:[Sdoi2013]项链
思路:首先考虑如何求珠子个数,一个珠子由a,b,c三个数组成且属于区间[1,a],并满足gcd(a,b,c)=1。由于要求本质相同,对于a,b,c这样的一个无序的数列且满足gcd(a,b,c)=1,设其总方案数为t1,那么显然本质相同的重复了6次,即(a,b,c),(a,c,b),(b,a,c),(b,c,a),(c,a,b),(c,b,a),所以要将t1/=6,但如果存在两个数相同,这样的其实只出现了三次,因此还要加上3*这样的情况(设其为t2)的方案数,同时可能有三个相同,这样的情况只可能是(1,1,1),只出现了一次,又因为计算两个数相同时已经加了三次,所以要再加两次。
即珠子个数=t1+3*t2+2。t1,t2的求法要用到莫比乌斯反演

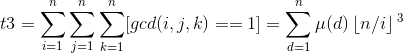
这个预处理mu可以sqrt(a)处理,然后考虑如何统计答案,联系bzoj4330爱之项链,那个题因为有特殊的东西使得不需要考虑是否本质不同,但本题是要考虑的,可以利用burnside引理,当旋转i格时,一共有gcd(n,i)个循环,且所有循环都是相邻的,这就相当于只考虑这长为gcd(n,i)的一段的合法的方案数,因为这样的话其余部分均可通过这一段置换得到,且本质相同。那这一段合法方案数有哪些呢,首先不仅相邻的不能相同,首尾也不能相同,因为置换后首就和尾相邻了,那么这不就变成了一个环且相邻颜色不同的总方案数了吗,设长为x的环的答案为f(x),于是最终答案即sigma(f(gcd(n,i)))。(f(x)=(m-1)^x+(x&1?1-m:m-1),m为颜色种类数,具体证明见http://www.cnblogs.com/DUXT/p/5951747.html
然后具体实现过程注意两个细节,一个vfk加强了数据,n有可能是p的倍数,因此不能直接求逆元,处理方法就是对求分子的过程中都对p^2取模,然后分子除以p,再乘以n/p在模p意义下的逆元即可,蒟蒻并不知道这是为什么。。。。。(当且仅当n是p的倍数是才能这么做)
然后可能出现long long*long long%long long,用一个乘爆的小技巧即可(详见函数mul())。
#include<iostream>
#include<cstdio>
using namespace std;
#define maxn 10001005 int cases,a,tot,p=1000000007;
int prime[maxn],mu[maxn],phi[maxn];
bool bo[maxn];
long long n,mod; long long mul(long long x,long long y){
long double t2=(long double)x*y/mod;
long long t1=x*y,t3=(long long)(t1-(long long)t2*mod)%mod;
return (t3+mod)%mod;
} long long power(long long a,long long k){
if (k==0) return 1;
if (k==1) return a%mod;
long long x=power(a,k/2),ans=mul(x,x);
if (k&1) ans=mul(ans,a);
return ans;
} long long fphi(long long x){
if (x<maxn) return phi[x];
long long ans=x;
for (int i=2;1ll*i*i<=x;i++)
if (x%i==0){
ans=ans-ans/i;
while (x%i==0) x/=i;
}
if (x!=1) ans=ans-ans/x;
return ans;
} long long solve(long long m,long long n){
return ((power(m-1,n)+(n&1?1ll-m:m-1ll))%mod+mod)%mod;
} void ex_gcd(long long a,long long b,long long &x,long long &y){
if (!b){x=1,y=0;return;}else ex_gcd(b,a%b,x,y);
long long x1=x,y1=y;
x=y1,y=x1-a/b*y1;
} long long inv(long long a){
long long x=0,y=0;ex_gcd(a,p,x,y);return (x%p+p)%p;
} int main(){
scanf("%d",&cases);mu[1]=1,phi[1]=1;
for (int i=2;i<maxn;i++){
if (!bo[i]) prime[++tot]=i,mu[i]=-1,phi[i]=i-1;
for (int j=1;j<=tot && i*prime[j]<maxn;j++){
bo[i*prime[j]]=1;
if (i%prime[j]==0){
mu[i*prime[j]]=0;
phi[i*prime[j]]=phi[i]*prime[j];
break;
}
mu[i*prime[j]]=-mu[i],phi[i*prime[j]]=phi[i]*(prime[j]-1);
}
}
for (int i=2;i<maxn;i++) mu[i]+=mu[i-1];
while (cases--){
scanf("%lld%d",&n,&a);long long ans2=0,ans3=0;
if (n%p==0) mod=1ll*p*p;else mod=p;
for (int i=1,j;i<=a;i=j+1){
j=a/(a/i);
ans2=(ans2+mul((mu[j]-mu[i-1]),(1ll*(a/i)*(a/i)%mod)))%mod;
ans3=(ans3+mul((mu[j]-mu[i-1]),mul(1ll*(a/i)*(a/i)%mod,(a/i)%mod)))%mod;
}
long long m=mul((ans3+3*ans2%mod+2)%mod,power(6,1ll*p*(p-1)-1)),ans=0;
for (int i=1;1ll*i*i<=n;i++)
if (n%i==0){
ans=(ans+mul(solve(m,i),fphi(n/i)))%mod;
if (1ll*i*i!=n) ans=(ans+mul(solve(m,n/i),fphi(i)))%mod;
}
if (n%p!=0) ans=mul(ans,power(n,mod-2))%p;
else ans=ans/p,n=n/p,ans=mul(ans,inv(n))%p;
printf("%lld\n",ans);
}
return 0;
}
UPD:一年以后来复习的时候发现后面这个也会证了。。。。。
首先x/y(mod p)=x(mod yp)/p,当且仅当y|x时成立。
证明:令x/y=kp+m,即x=kyp+mp,然后有x=mp(mod yp),即x/p=m(mod yp),m就是x/y(mod p)。
然后此题的y=n,且满足y|x,然后用上面的那个公式就能得出以前的那个结论了。。。。。
bzoj3202:[Sdoi2013]项链的更多相关文章
- BZOJ3202 [Sdoi2013]项链
Problem E: [Sdoi2013]项链 Time Limit: 30 Sec Memory Limit: 512 MBSubmit: 427 Solved: 146[Submit][Sta ...
- 【BZOJ3202】项链(莫比乌斯反演,Burnside引理)
[BZOJ3202]项链(莫比乌斯反演,Burnside引理) 题面 BZOJ 洛谷 题解 首先读完题目,很明显的感觉就是,分成了两个部分计算. 首先计算本质不同的珠子个数,再计算本质不同的项链个数. ...
- bzoj 3202: [Sdoi2013]项链
Description 项链是人体的装饰品之一,是最早出现的首饰.项链除了具有装饰功能之外,有些项 链还具有特殊显示作用,如天主教徒的十字架链和佛教徒的念珠. 从古至今人们为了美化人体本身,也美 化环 ...
- 洛谷P3307 [SDOI2013]项链 [polya定理,莫比乌斯反演]
传送门 思路 很明显的一个思路:先搞出有多少种珠子,再求有多少种项链. 珠子 考虑这个式子: \[ S3=\sum_{i=1}^a \sum_{j=1}^a\sum_{k=1}^a [\gcd(i,j ...
- [SDOI2013]项链
description luogu 最近,铭铭迷恋上了一种项链.与其他珍珠项链基本上相同,不过这种项链的珠子却与众不同,是正三菱柱的泰山石雕刻而成的. 三菱柱的侧面是正方形构成的,上面刻有数字. 能够 ...
- 洛谷 P3307: bzoj 3202: [SDOI2013] 项链
题目传送门:洛谷P3307.这题在bzoj上是权限题. 题意简述: 这题分为两个部分: ① 有一些珠子,每个珠子可以看成一个无序三元组.三元组要满足三个数都在$1$到$m$之间,并且三个数互质,两个珠 ...
- Luogu3307:[SDOI2013]项链
传送门 求每个珠子的方案数 即有序的求三元组 \((x,y,z),x,y,z\le a\) 满足 \(gcd(x,y,z)=1\) 设 \(G_i\) 表示 \(i\) 个小于等于 \(a\) 的有序 ...
- bzoj 3202 [Sdoi2013]项链——容斥+置换+推式子
题目:https://www.lydsy.com/JudgeOnline/problem.php?id=3202 可见Zinn博客:https://www.cnblogs.com/Zinn/p/100 ...
- 洛谷 P3307 - [SDOI2013]项链(Burnside 引理+数论)
题面传送门 看到题目我们显然可以将题目拆分成两部分:首先求出有多少个符合要求的珠子 \(c\),这样我们就可以将每种珠子看成一种颜色,题目也就等价于有多少种用 \(c\) 种颜色染长度为 \(n\) ...
随机推荐
- 【Java基础】继承的一些总结
什么是继承 把一些类的具有共性的东西剥离出来形成一个新的类,然后各个其他类保留自己独有的特性,并用关键字extends继承这个剥离出来的新的类,可以最终达到各类原始相同效果,但是在每个类中,单用一个“ ...
- HDOJ-ACM1011(JAVA)
转载声明:原文转自:http://www.cnblogs.com/xiezie/p/5569721.html 搞懂题意之后,个人感觉,这道题题目的描述相当的费解~ 做这道题目,个人感觉,涉及到树的遍历 ...
- 问题-[Delphi]通过Map文件查找内存地址出错代码所在行
一 什么是MAP文件 什么是 MAP 文件?简单地讲, MAP 文件是程序的全局符号.源文件和代码行号信息的唯一的文本表示方法,它可以在任何地方.任何时候使用,不需要有额外的程序进行支持 ...
- poj 1144 Network【双连通分量求割点总数】
Network Time Limit: 1000MS Memory Limit: 10000K Total Submissions: 11042 Accepted: 5100 Descript ...
- 利用ACE 自己实现的线程池
1: 线程池组件的配置文件: [log] ;DEBUG = 0 ;INFO = 1 ;WARN = 2 ;FAULT = 3 level=0 ;SCREENOUT = 0 ;FILEOUT = 1 ; ...
- Robotium学习笔记二
一. 控制测试用例的执行顺序 采用TestSuit方式来控制每条Case的运行顺序 Demo如下 public static Test suite() { TestSuite suite = new ...
- Windows上常见的集中布尔类型的比较
博客搬到了fresky.github.io - Dawei XU,请各位看官挪步.最新的一篇是:Windows上常见的集中布尔类型的比较.
- Linux内核分析:页回收导致的cpu load瞬间飙高的问题分析与思考--------------蘑菇街技术博客
http://mogu.io/156-156 摘要 本文一是为了讨论在Linux系统出现问题时我们能够借助哪些工具去协助分析,二是讨论出现问题时大致的可能点以及思路,三是希望能给应用层开发团队介绍一些 ...
- linux上安装memcached
我的版本为Centos Release 5.3 (Final)使用这个命令可以知道你的Linux版本1.cat /etc/redhat-release首先要安装libevent库.cd /usr/lo ...
- 第一个felx项目的创建
使用新建flex项目向导建立项目
