标准差（standard deviation）和标准误差（standard error）你能解释清楚吗？

by：ysuncn（欢迎转载，请注明原创信息）

什么是标准差（standard deviation）呢？依据国际标准化组织（ISO）的定义：标准差σ是方差σ²的正平方根；而方差是随机变量期望的二次偏差的期望，这个就不用解释了。

什么是标准误差（standard error）呢？看了些文献，有的还是大牛的，定义都不统一，通常来说有两种定义方式：

1、样本容量为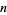的标准误差是样本的标准差除以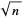。ps：这里还有人用样本的标准差除以n来作为标准误差（预计是弄错了，只是标准误差是基于整体均值来预计标准差，所以也没有必要说人家错）；
       2、一个统计量的标准误差还能够用预计误差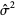的标准差来刻画即：。

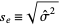下边来自编辑学报郝拉娣的《标准差与标准误》，相关性也比較大，希望对大家有帮助。

标准差作为随机误差(或真差) 的代表,是随机误差绝对值的统计均值。在国家计量技术规范中,标准差的正式名称是标准偏差,简称标准差,用符号σ表示。标准差的名称有10 余种,如整体标准差、母体标准差、均方根误差、均方根偏差、均方误差、均方差、单次測量标准差和理论标准差等。标准差的定义式为：用样本标准差s 的值作为整体标准差σ的预计值。样本标准差的计算公式为：。

在抽样试验(或反复的等精度測量) 中, 经常使用到样本平均数的标准差,亦称样本平均数的标准误或简称标准误( standard error of mean) 。由于样本标准差s 不能直接反映样本平均数…x 与整体平均数μ到底误差多少, 所以, 平均数的误差实质上是样本平均数与整体平均数之间的相对误。可推出样本平均数的标准误为，其预计值为，它反映了样本平均数的离散程度。标准误越小, 说明样本平均数与整体平均数越接近,否则,表明样本平均数比較离散。

标准差是表示个体间变异大小的指标,反映了整个样本对样本平均数的离散程度,是数据精密度的衡量指标;而标准误反映样本平均数对整体平均数的变异程度,从而反映抽样误差的大小 ,是量度结果精密度的指标。

參考：http://mathworld.wolfram.com/StandardError.html……