程序员必会算法-KMP算法

KMP算法是一种优秀的字符串匹配算法，字符串匹配的常规算法是一步一步进行移位和比较操作，直至找到完全相匹配的字符串。

下面通过一个例子，为大家仔细说明KMP算法的使用和思路：

问题：

　　在字符串“DEABCDABABCDABCDABDE”字符串中，匹配字符串"ABCDABD".

算法思路：

　　KMP算法的思路在于，根据已经匹配的部分字符的信息，不把搜索位置移回已经比较过的位置，这样就提高了效率，是不是还是有点不清楚？没关系，让我们来根据一个例子来切实体会一下KMP算法是如何实现的。

图解：

1、KMP算法的核心是一张“部分匹配表”，这个表是怎么来的，后面再说，先用了再说，下图就是该问题的部分匹配表。

这个表上面一行是我们的模式字符串，下面一行是每个字符所对应的匹配值

移位规则是 移动位数 = 已匹配的字符串长度 - 已匹配字符串的最后一位字符所对应的匹配值。

2、接下来就开始进行操作

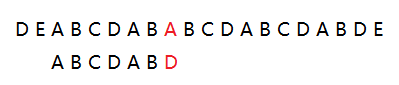
上图中我们看到，移位两位后，我们找到了部分匹配的字符串"ABCDAB"，但并没有找到完全匹配的字符串，如果是常规思路，就是在继续往下一步一步移位，但我们这里不这样进行，我们观察到，已经匹配的字符串长度是6，匹配到的最后一个字符是"B",查询部分匹配表，这个“B”的部分匹配值是2，那么根据我们算法的移位规则，下一步我们的移位长度 = 6 - 2 = 4；

3、

╮(╯▽╰)╭，有没有发现，移了4位之后，刚好到达了下一个“AB”处？是不是很神奇？好了，打住，我们继续往下移，当前已匹配的字符串长度为2，查询这个“B”的匹配值为0（别和上个B搞混了），根据算法，我们接下来移位长度是 2 - 0 = 2；

4、

继续，和前面的步骤相同，我们这次移位长度为 6 - 2 = 4；

5、

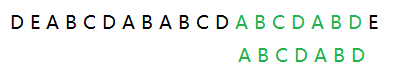
至此，我们已经找到了完全匹配的字符串，当然，如果母字符串的长度较长，我们可以继续进行移位，继续寻找，和之前的步骤相同，下次我们移位长度为 7 - 0 = 7。

算法分析：

　　不知道大家看到现在，有没有一点明悟？来，让我们分析一下模式字符串“ABCDABD”：

　　对于搜索来说，我们首先关注的肯定是第一个字符，如果第一个字符都不匹配，那么后面的字符就没有比较的必要了，该目标字符串的第一个字符是’A‘，让我们看看这个字符串里有没有’A‘，诶，还真有，假如说我们现在已经匹配了“ABCDA”，5个字符，我们要移4位才能从第一个'A'移到第二个'A'，’A‘只有一个字符，5 - 1 = 4;

　　再往下看，关注完第一个字符，我们开始关注和第一个字符依次相连的子字符串，这些字符串有一个共性，就是第一个字符都是’A‘，那我们看看这种字符串能有多少，"AB","ABC","ABCD","ABCDA","ABCDAB","ABCDABD"，再看看这些字符串在目标字符串“ABCDABD”中存在几个，可以看出，除去和第一个“A”相连的，“AB”还有一个，其余的没有，而"AB"长度为2，所以在表中，第二个B的匹配值为2。

该算法的核心思路在于，有时候，字符串的头部和尾部可能会有重复。

　　不知道大家有没有听懂？让我们把匹配字符串换一下，换成“ABCDABC”，现在的部分匹配表应该是：

　　

算法思考和延伸：

　　如果模式字符串过长，部分匹配表的生成会占用较多的时间，如何去提高部分匹配表的生成效率，是该算法的优化所在。（个人观点，如有大佬，请指教！）

　　该算法思想和字典编码有一定的相通之处。改天我会写出一个字典编码的文章。敬请期待！