【洛谷P3389 【模板】高斯消元法】

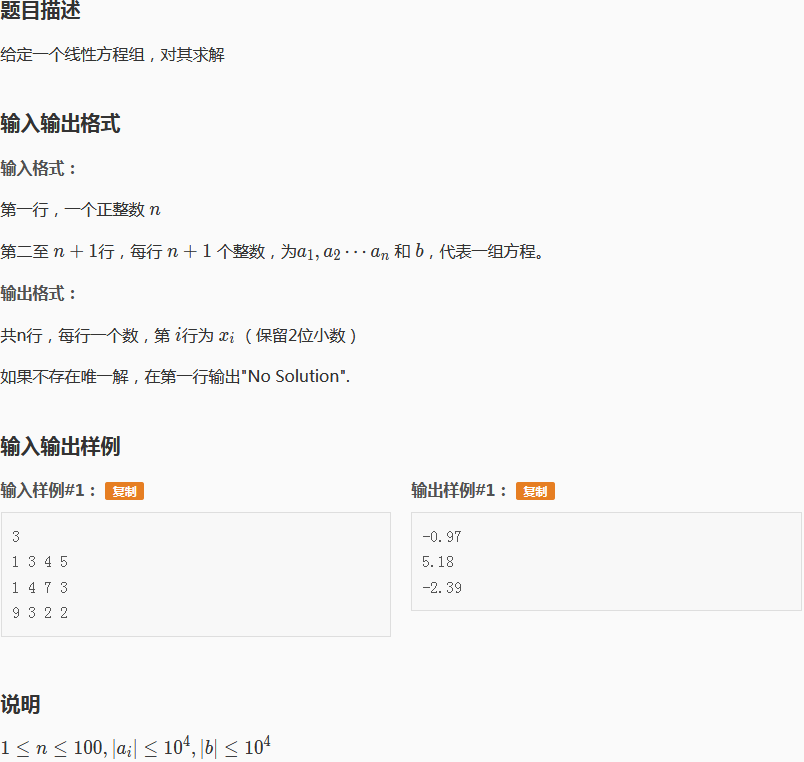
这是个版子题，当然本蒟蒻也是看了好几天才明白

对于这样的线性方程组，我们可以看成是一个矩阵

对于百度百科给的定义（我感到很迷）赶脚和行列式有的一拼

但我们要注意的是：

行列式是一个确切的值（有关行列式求值，下片博文再说），可以看做是一个数值；

而矩阵不同，矩阵是一个数表，无特殊的值。当然，性质也略有不同（这里就先不细讲了）

高斯消元的核心就是把这个n*n的矩阵消成一个对角矩阵（就是除了a【i】【i】为1以外，其余全为零但是不要乱划a【i】【n+1】这是我们要输出的东西）然后就ok了

其中一些性质可以通过度娘或下面的（李昊的）过程代码验证一下

//这不是AC代码，只是一个检测的（黈力的小心一点啊QAQ）
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<cstdlib>
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<int,int> pr;
const double pi=acos(-);
#define rep(i,a,n) for(int i=a;i<=n;i++)
#define per(i,n,a) for(int i=n;i>=a;i--)
#define Rep(i,u) for(int i=head[u];i;i=Next[i])
#define clr(a) memset(a,0,sizeof a)
#define pb push_back
#define mp make_pair
#define fi first
#define sc second
ld eps=1e-;
ll pp=;
ll mo(ll a,ll pp){if(a>= && a<pp)return a;a%=pp;if(a<)a+=pp;return a;}
ll powmod(ll a,ll b,ll pp){ll ans=;for(;b;b>>=,a=mo(a*a,pp))if(b&)ans=mo(ans*a,pp);return ans;}
ll read(){
    ll ans=;
    char last=' ',ch=getchar();
    while(ch<'' || ch>'')last=ch,ch=getchar();
    while(ch>='' && ch<='')ans=ans*+ch-'',ch=getchar();
    if(last=='-')ans=-ans;
    return ans;
}
//head
int n,m;
double a[][];

bool check(int k){
    if(fabs(a[k][n+])<eps)return ;
    rep(i,,n)
        if(fabs(a[k][i])>eps)return ;
    return ;
}
int main(){
    freopen("1.txt","r",stdin);
    n=read();m=read();
    // a_i,1 a_i,2 ... a_i,n a_i,n+1
    rep(i,,m)
        rep(j,,n+)a[i][j]=read();
    rep(j,,m){
            rep(k,,n+)cout<<a[j][k]<<" ";
            puts("");
        }
    int flag=;
    rep(i,,n){
        int t=i;
        while(a[t][i]== && t<=n)t+=;
        if(t==n+){
            flag=;
            continue;
        }
        rep(j,,n+)swap(a[i][j],a[t][j]);
        double kk=a[i][i];
        rep(j,,n+)a[i][j]/=kk;
        rep(j,,m)
            if(i!=j){
                double kk=a[j][i];
                rep(k,,n+)
                    a[j][k]-=kk*a[i][k];
            }
        puts("------------");
        rep(j,,m){
            rep(k,,n+)cout<<a[j][k]<<" ";
            puts("");
        }
    }
    if(flag){
        rep(i,,m)
            if(!check(i)){
                printf("No solution\n");
                return ;
            }
        printf("So many solutions\n");
    }

}

通过这个代码，可以看到化简的每一步过程

下面才是真正的AC代码：

//真正的AC代码
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
int n,s;
double a[][];
int main()
{
    cin>>n;
    for(int i=;i<=n;i++)//输入矩阵
       for(int j=;j<=n+;j++)//别忘记最后那一列
       　　cin>>a[i][j];
    for(int i=;i<=n;i++)
    {
        s=i;
        while(a[s][i]==&&s<=n)
        s++;
        if(s==n+)
        {
            cout<<"No Solution";//判是否有解（若有一行或一列全为0，则无解）
            return ;
        }
        for(int j=;j<=n+;j++)
            swap(a[i][j],a[s][j]);
        double k=a[i][i];
        for(int j=;j<=n+;j++)
            a[i][j]=a[i][j]/k; //为防止a【i】【i】为零，可以换一下
        for(int j=;j<=n;j++)
        {
            if(i!=j)
            {
                double ki=a[j][i];
                for(int m=;m<=n+;m++)
                    a[j][m]=a[j][m]-ki*a[i][m];//这就保证可以将除了a【i】【i】的全部为0
            }
        }
    }
    for(int i=;i<=n;i++)
        printf("%.2lf\n",a[i][n+]);//输出ouo
    return ;
}

这其中用到了一些神奇的性质，还是提前掌握为妙