什么是卷积convolution

定义

卷积是两个变量在某范围内相乘后求和的结果。如果卷积的变量是序列x(n)和h(n)，则卷积的结果

，

其中星号*表示卷积。

当时序n=0时，序列h(-i)是h(i)的时序i取反的结果；时序取反使得h(i)以纵轴为中心翻转180度，所以这种相乘后求和的计算法称为卷积和，简称卷积。

另外，n是使h(-i)位移的量，不同的n对应不同的卷积结果。

如果卷积的变量是函数x(t)和h(t)，则上述卷积(和)的计算变为积分：

，

其中p是积分变量，积分也是求和，t是使函数h(-p)位移的量，星号*表示卷积。

参考《数字信号处理》杨毅明著，p.55、p.188、p.264，机械工业出版社2012年发行。

图解卷积

首先将两个函数都用来表示。
对其中一个函数做水平翻转： →
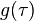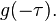
加上一个时间偏移量，让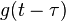能沿着轴滑动。
让t从-∞滑动到+∞。两函数交会时，计算交会范围中两函数乘积的积分值。
换句话说，我们是在计算一个滑动的的加权平均值。也就是使用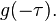当做加权函数，来对取加权平均值。

最后得到的波形（未包含在此图中）就是f和g的卷积。

如果f(t)是一个单位脉冲，我们得到的乘积就是g(t)本身，称为冲激响应。

性质

交换律结合律分配律数乘结合律其中a为任意实数（或复数）。

微分定理其中Df表示f的微分，如果在离散域中则是指差分算子，包括前向差分与后向差分两种。

卷积定理

卷积定理指出，函数卷积的傅里叶变换是函数傅里叶变换的乘积。即，一个域中的卷积相当于另一个域中的乘积，例如时域中的卷积就对应于频域中的乘积。

F(g(x)*f(x)) = F(g(x))F(f(x))

其中F表示的是傅里叶变换。

这一定理对拉普拉斯变换、双边拉普拉斯变换、Z变换、Mellin变换和Hartley变换（参见Mellin inversion theorem）等各种傅里叶变换的变体同样成立。

在调和分析中还可以推广到在局部紧致的阿贝尔群上定义的傅里叶变换。

利用卷积定理可以简化卷积的运算量。

对于长度为n的序列，按照卷积的定义进行计算，需要做2N - 1组对位乘法，其计算复杂度为O(N * N)；

而利用傅里叶变换将序列变换到频域上后，只需要一组对位乘法，利用傅里叶变换的快速算法之后，总的计算复杂度为O(N * log N)。

这一结果可以在快速乘法计算中得到应用。

应用

卷积在工程和数学上都有很多应用：

统计学中，加权的滑动平均是一种卷积。
概率论中，两个统计独立变量X与Y的和的概率密度函数是X与Y的概率密度函数的卷积。
声学中，回声可以用源声与一个反映各种反射效应的函数的卷积表示。
电子工程与信号处理中，任一个线性系统的输出都可以通过将输入信号与系统函数（系统的冲激响应）做卷积获得。
物理学中，任何一个线性系统（符合叠加原理）都存在卷积。

招展

卷积是一种线性运算,图像处理中常见的mask运算都是卷积，广泛应用于图像滤波。Kenneth R.Castlman的《数字图像处理》对卷积讲得很详细。

高斯变换就是用高斯函数对图像进行卷积。高斯算子可以直接从离散高斯函数得到：

for(i=0; i<N; i++)

{

for(j=0; j<N; j++)

{

g[i*N+j]=exp(-((i-(N-1)/2)^2+(j-(N-1)/2)^2))/(2*delta^2));

sum += g[i*N+j];

}

再除以 sum 得到归一化算子 ,N是滤波器的大小，delta自选

首先，在提到卷积之前，必须提到卷积出现的背景。

卷积是在信号与线性系统的基础上或背景中出现的，脱离这个背景单独谈卷积是没有任何意义的，除了那个所谓褶反公式上的数学意义和积分（或求和，离散情况下）。

信号与线性系统，讨论的就是信号经过一个线性系统以后发生的变化（就是输入输出和所经过的所谓系统，这三者之间的数学关系）。所谓线性系统的含义，就是，这个所谓的系统，带来的输出信号与输入信号的数学关系式之间是线性的运算关系。

因此，实际上，都是要根据我们需要待处理的信号形式，来设计所谓的系统传递函数，那么这个系统传递函数和输入信号，在数学上的形式就是所谓的卷积关系。

卷积关系最重要的一种情况，就是在信号与线性系统或数字信号处理中的卷积定理。

利用该定理，可以将时间域或空间域中的卷积运算等价为频率域的相乘运算，从而利用FFT等快速算法，实现有效的计算，节省运算代价。

C++代码