BZOJ5104 Fib数列（二次剩余+BSGS）

　　5在1e9+9下有二次剩余，那么fib的通项公式就有用了。

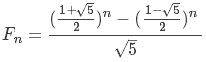　　已知Fn，求n。注意到[(1+√5)/2]·[(1-√5)/2]=-1，于是换元，设t=[(1+√5)/2]ⁿ，原式变为√5·Fn=t-(-1)ⁿ·t^-1。同乘t并移项，可得t²-√5·Fn·t-(-1)ⁿ=0。讨论n的奇偶性，BSGS求二次剩余大力解方程即可。用BSGS求二次剩余是非常简单的，求出其以原根为底的离散对数即可。

　　注意二次剩余有正负两解，但似乎代进去正根（即√g^k=g^k/2）就行了，不太明白。以及题目要求最小解，BSGS的时候注意顺序。还有BSGS不一定有解，我也不知道我在BSGS里面assert了半天是在干啥。调了一年惨炸了。

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstdlib>
#include<cstring>
#include<algorithm>
#include<map>
#include<cassert>
using namespace std;
#define ll long long
#define P 1000000009
char getc(){char c=getchar();while ((c<'A'||c>'Z')&&(c<'a'||c>'z')&&(c<''||c>'')) c=getchar();return c;}
int gcd(int n,int m){return m==?n:gcd(m,n%m);}
int read()
{
    int x=,f=;char c=getchar();
    while (c<''||c>'') {if (c=='-') f=-;c=getchar();}
    while (c>=''&&c<='') x=(x<<)+(x<<)+(c^),c=getchar();
    return x*f;
}
int n,b,g,v,ans=P;
map<int,int> f;
int ksm(int a,int k)
{
    int s=;
    for (;k;k>>=,a=1ll*a*a%P) if (k&) s=1ll*s*a%P;
    return s;
}
int inv(int a){return ksm(a,P-);}
int BSGS(int g,int k)
{
    f.clear();
    int block=sqrt(P),t=ksm(g,block),x=,ans=-;g=inv(g);
    for (int i=;i<block;i++)
    {
        if (f.find(1ll*x*k%P)==f.end()) f[1ll*x*k%P]=i;
        x=1ll*x*g%P;
    }
    x=;
    for (int i=;i<P;i+=block)
    {
        if (f.find(x)!=f.end()) {ans=f[x]+i;break;}
        x=1ll*x*t%P;
    }
    return ans;
}
int SQRT(int n)
{
    int k=BSGS(g,n);
    if (k==-||k&) return -;
    return ksm(g,k>>);
}
void solve(int c,int op,int op2)
{
    int delta=SQRT(((1ll*b*b-4ll*c)%P+P)%P);
    if (delta==-) return;
    delta=(P+op2*delta)%P;
    int ans1=1ll*((delta-b)%P+P)%P*inv()%P,ans2=1ll*((-delta-b)%P+P)*inv()%P;
    ans1=BSGS(v,ans1),ans2=BSGS(v,ans2);
    if ((ans1&)==op&&ans1>) ans=min(ans,ans1);
    if ((ans2&)==op&&ans2>) ans=min(ans,ans2);
}
int fib(int n)
{
    struct matrix
    {
        int n,a[][];
          matrix operator *(const matrix&b) const
           {
            matrix c;c.n=n;memset(c.a,,sizeof(c.a));
            for (int i=;i<n;i++)
                for (int j=;j<;j++)
                    for (int k=;k<;k++)
                    c.a[i][j]=(c.a[i][j]+1ll*a[i][k]*b.a[k][j])%P;
            return c;
        }
    }f,a;
    f.n=;f.a[][]=,f.a[][]=;
    a.n=;a.a[][]=,a.a[][]=a.a[][]=a.a[][]=;
    for (;n;n>>=,a=a*a) if (n&) f=f*a;
    return f.a[][];
}
void work(int sqrt5)
{
    b=(P-1ll*sqrt5*n%P)%P;
    v=1ll*(sqrt5+)*inv()%P;
    solve(P-,,),solve(,,);
    //solve(P-1,0,-1),solve(1,1,-1);
}
int main()
{
#ifndef ONLINE_JUDGE
    freopen("bzoj5104.in","r",stdin);
    freopen("bzoj5104.out","w",stdout);
    const char LL[]="%I64d\n";
#else
    const char LL[]="%lld\n";
#endif
    /*for (int i=2;;i++)
    {
        bool flag=1;
        for (int j=2;j*j<P;j++)
        if ((P-1)%j==0)
        {
            if (ksm(i,j)==1) {flag=0;break;}
            if (ksm(i,(P-1)/j)==1) {flag=0;break;}
        }
        if (flag) {g=i;break;}
    }*/
    g=;
    n=read();
    work(SQRT());//,work(P-SQRT(5));
    if (ans==P) cout<<-;else assert(fib(ans)==n),cout<<ans;
    return ;
}