HDU3988-Harry Potter and the Hide Story（数论-质因数分解）

Harry Potter and the Hide Story

Time Limit: 10000/5000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)

Total Submission(s): 2193    Accepted Submission(s): 530

Problem Description

iSea is tired of writing the story of Harry Potter, so, lucky you, solving the following problem is enough.

 

Input

The first line contains a single integer T, indicating the number of test cases.

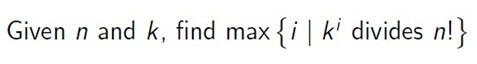
Each test case contains two integers, N and K. 



Technical Specification



1. 1 <= T <= 500

2. 1 <= K <= 1 000 000 000 000 00

3. 1 <= N <= 1 000 000 000 000 000 000

 

Output

For each test case, output the case number first, then the answer, if the answer is bigger than 9 223 372 036 854 775 807, output “inf” (without quote).

 

Sample Input

2
2 2
10 10

 

Sample Output

Case 1: 1
Case 2: 2

 

Author

iSea@WHU

 

题意：给你n和k,让你求出最大的i 满足n的阶乘能被k的i次方整除。

思路:对k进行质因数分解。求出每一个质因数在阶乘中的幂的大小。答案即为最小的那个幂。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <string>
#include <algorithm>
#include <queue>
using namespace std;

#define LL unsigned long long

const int maxn = 10000005;
bool isPrime[maxn];
vector<LL> prime,digit,cnt;

void getPrime(){
    prime.clear();
    memset(isPrime,0,sizeof isPrime);
    for(LL i = 2; i < maxn; i++){
        if(!isPrime[i]){
            prime.push_back(i);
            for(LL j = i*i; j < maxn; j += i)
                isPrime[j] = 1;
        }
    }
}

void getDigit(LL k){

    for(int i = 0; i < prime.size() && k >= prime[i]; i++){
        if(k%prime[i]==0){
            int tt = 0;
            digit.push_back(prime[i]);
            while(k%prime[i]==0){
                tt++;
                k /= prime[i];
            }
            cnt.push_back(tt);
        }
    }
    if(k!=1){
        digit.push_back(k);
        cnt.push_back(1);
    }
}

LL getSum(LL n,LL p){
    LL res = 0;
    while(n){
        n /= p;
        res += n;
    }
    return res;
}
int main(){
    int ncase,T=1;
    LL k,n;
    getPrime();
    cin >> ncase;
    while(ncase--){
        cin >> n >> k;
        if(k==1){
            printf("Case %d: inf\n",T++);
            continue;
        }
        LL ans = -1;
        digit.clear();
        cnt.clear();
        getDigit(k);

        for(int i = 0; i < digit.size(); i++){
            LL tk = getSum(n,digit[i])/cnt[i];
            if(ans == -1) ans = tk;
            else ans = min(ans,tk);
        }
        printf("Case %d: %I64u\n",T++,ans);

    }
    return 0;
}

版权声明：本文博客原创文章。博客，未经同意，不得转载。