PTA 朋友圈 (25 分) 代码详解 （并查集）

1、题目要求：

某学校有N个学生，形成M个俱乐部。每个俱乐部里的学生有着一定相似的兴趣爱好，形成一个朋友圈。一个学生可以同时属于若干个不同的俱乐部。根据“我的朋友的朋友也是我的朋友”这个推论可以得出，如果A和B是朋友，且B和C是朋友，则A和C也是朋友。请编写程序计算最大朋友圈中有多少人。

输入格式:

输入的第一行包含两个正整数N（≤30000）和M（≤1000），分别代表学校的学生总数和俱乐部的个数。后面的M行每行按以下格式给出1个俱乐部的信息，其中学生从1~N编号：

第i个俱乐部的人数Mi（空格）学生1（空格）学生2 … 学生Mi

输出格式:

输出给出一个整数，表示在最大朋友圈中有多少人。

输入样例:

7 4
3 1 2 3
2 1 4
3 5 6 7
1 6

 

结尾无空行

输出样例:

4

 

结尾无空行

 

2、题目解析：

首先我们来理清一下题目意思，A和B是朋友，B和C是朋友，那么A和C也是朋友，如果此时C又和D是朋友，那么A和D也是朋友，则A此时与B，C，D都是朋友，那么这个以A为起点

的朋友圈就有4个人。又如测试用例，第一行表示第一个圈子，有1，2，3这3个人，第二个圈子有1，4这两个人，因为1和4是好朋友，所以4和2、3都是朋友，因此以1为中心的这个

朋友圈共有4个人。这是一个以朋友为传递关系建立成的朋友圈，是一种连通性的问题。简单来说就是求这几个连通分支里点最多的连通分支，朋友圈代表连通分支，朋友圈里

的人代表连通分支上的点。所以题目就是求以朋友关系连起来的最大的朋友圈（连通分支）里有几个人（点）。

 

3、代码：

#include <bits/stdc++.h>
using namespace std;
#define MAXn 30001
int fa[MAXn];
int num[30001];

int Find(int x){
    int r=x;
    while(r!=fa[r])
        r=fa[r];
    int i=x,temp;
    while(r!=fa[i]){
        temp=fa[i];
        fa[i]=r;
        i=temp;
    }
    return r;
}

void Union(int x,int y){
    int fx=Find(x),fy=Find(y);
    if(fx!=fy){
        fa[fx]=fy;
        num[fy]+=num[fx];
    }
}

int main(){
    int n,m,people,first,p;
    cin>>n>>m;
    for(int i=0;i<=n;i++)
        fa[i]=i;
    for(int i=0;i<=n;i++)
        num[i]=1;
    while(m--){
        cin>>people;
        cin>>first;
        while(--people){
            cin>>p;
            Union(first,p);
        }
    }
    int max=0;
    for(int i=0;i<=n;i++){
        if(num[i] > max)
            max=num[i];
    }
    cout<<max<<endl;
    return 0;
}

4、“并查集” 说明：

首先本题是属于数据结构中的 “并查集“ 类型的题目，所以要理解本题的代码，我们就要先弄懂什么是并查集。

所以现在，我们先来搞懂 ”并查集“是什么？

顾名思义，”并“就是合并，”查“就是查找，”集“就是集合（元素唯一）。”并查集"主要代码结构有两个函数，一个主函数“，一个函数是 Find(x) ，一个是 Union（x,y）。

将每个集合看成每棵树，用数组 fa[]  来存储各个节点的父节点，fa[i] 表示 i 的父节点。如下图1，fa[2] = 1，fa[3] = 1，fa[4] = 2......  （图论基础）

若每棵树只有一个节点，那么它的父节点就是它自己，即 fa[i] = i，谁和谁都没有关系，如图2。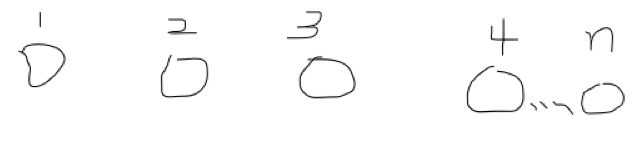

 合并：Union(x,y)

那么我们要怎么把它们建立联系呢，就是把单独的树合并成一颗大的树？

可以令每棵树的根节点都一样，那么它们就合并了，比如要将 图1中的1 和2 合并成一颗树，可以让1成为2的根节点（当然也可以让2成为1的根节点），

即 fa[2] = 1，fa[1] = 1，（fa[1] = 2，fa[2] = 2）这样就变成了图3.

，

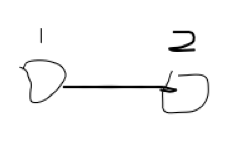若要将3也合并到1那颗树上，如图.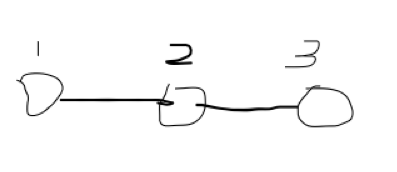可以知道fa[3] = 2， fa[2] = 1，fa[1] = 1，则把3合并过来的表达式：fa[3] = fa[1]，

假设x=2，y=3 ，将2和3合并，则 fa[x] = y ;

这就是将集合合并起来，从上面两个图中我们可以发现若1都是根节点，那么fa[1] = 1，若2是根节点，那么fa[2] = 2，即fa[i] = i 表示此时 i 是这颗树的根节点，

”查“就是查找根节点。

找到根节点有什么用？

查找：Find(x)

找到一颗树的根节点就相当于找到了这颗树的编号，换个说法说就是某个集合的编号，可以知道这个人在哪个集合里。

如下图

我们想找5属于哪颗树，就得一个一个父节点网上找，直到找到根节点 Find(5) = 1才知道5属于上面那颗树。如果我们想找8，那么我们必须找到8的根节点 Find(8) = 6

才知道8属于下面那棵树。

因此函数 Find(x) 就是查找 x的根节点，返回值是一个数（根节点）。

如果我想让5和6成为好朋友呢？只需要在5和6之间画一条线连起来，或者之间让6的父节点之接变成1，这样6就属于5的那颗树啦，如下图

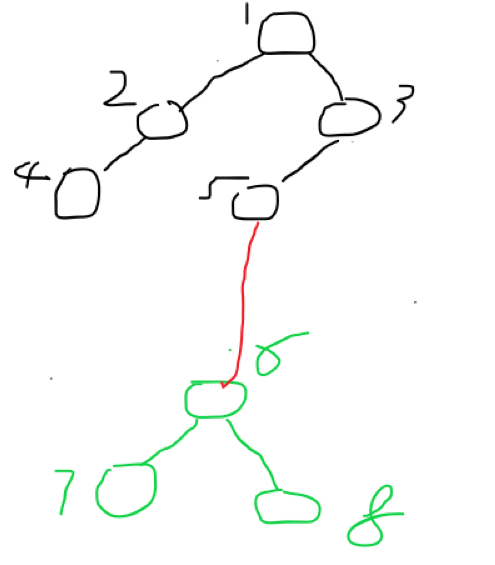或者这样也行，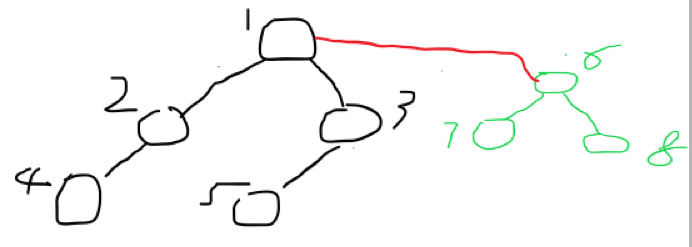

即让5的根节点等于6的根节点，因此合并的原理就是：查找x和y 的根节点，fx = Find(x) , fy = Find(y) ；令y的根节点等于x的根节点，Find(fx) = fy。

说到这，想必都清楚”并“和”查“的意思了吧？不知道我说得清楚了没？文案和图有点乱。。。。

还有一点要注意的是，还有个"路径压缩"，这个 “路径压缩” 是啥捏？

举个例子：如下图

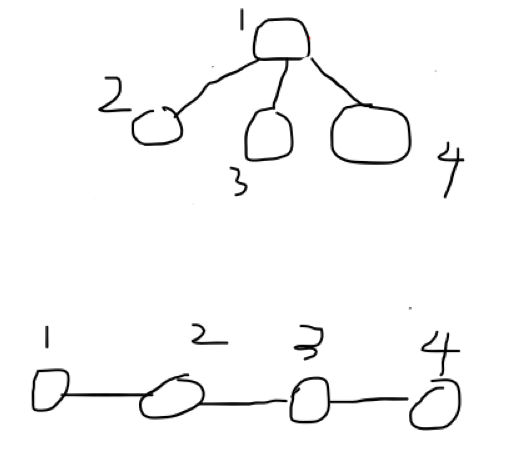
假设1是根节点，（不分是否二叉树）， 如果我们要找3的根节点是谁，那么上面图的做法是 fa[3] = 1，查找一次就找到了。而下面图的做法是 fa[3] = 2，不是根节点（怎么判断是不是根节点上文有说），

再查找 fa[2] = 1 找到了，是不是上面图的做法查询的速度会更快一点？如果有n个节点，那么下面图要查找n-1次了，此时效率比较低。所以“路径压缩” 就是要把树（集合）上的

节点都搞成上面图的样子，这样就缩短了查询根节点的路径了。

5、代码解析：

了解了“并查集 " ，那么我们现在就来看看本题的代码怎么实现吧！

#include <bits/stdc++.h>
using namespace std;
#define MAX 30001
int fa[MAX];//存储父节点
int num[30001];//存储节点数

/*查找根节点*/
int Find(int x){
    //找x的根节点
    int r=x;//x赋给r，以免中间发生变化后x改变
    while(r!=fa[r])//循环直到找到根节点，上文第4点有说例子
        r=fa[r];//让r的父节点等于r，直到找到x的根节点,此时就可返回r了，下面是为了压缩路径写的代码
    //路径压缩
    int i=x,temp;//temp为中间变量
    while(r!=fa[i]){//假设链式树，“1---2---3---4” 根节点r=1，x=3，即要把3直接套在1后面，这里上文“路径压缩”有说到。
        temp=fa[i];//把3的父节点2赋给temp
        fa[i]=r;//让3的父节点等于1
        i=temp;//把3的父节点2赋给i,继续循环把2的根节点变成1
    }
    return r;//最后返回根节点r
}

/*合并两个集合*/
void Union(int x,int y){
    int fx=Find(x),fy=Find(y);//分别找到x和y的根节点
    if(fx!=fy){//如果x和y的根节点不一样，说明两个人不在一棵树上，此时就要合并两个人
        fa[fx]=fy;//让y的根节点fy成为x的根节点，两棵树（集合）就合并了
        num[fy]+=num[fx];//fy这颗树多加num[fx]个人,num[fx]代表以fx为根节点所在的树上有几个节点
    }
}

int main(){
    int n,m,people,first,p;
    cin>>n>>m;
    //给每个人编号，并让每个人的父节点都是自己
    for(int i=0;i<=n;i++)
        fa[i]=i;
    //定义一个num[]数组来存储第i棵树（朋友圈）上有几个节点（人），刚开始都是一个人，所以初始化为1
    for(int i=0;i<=n;i++)
        num[i]=1;
    //输入数据
    while(m--){
        cin>>people;//每一行中第一个数是这个圈子有几个人
        cin>>first;//第二个数在这里输入，是为了将第一个数作为每一行（每一个圈子）的根，用来标识朋友圈加以区别
        while(--people){
            cin>>p;//依次输入每个人的编号
            Union(first,p);//每输入一个人就合并到第一个人的树（圈子）上，这样每一行的人都代表一个圈子里的人
        }
    }
    //求出最大的树（圈子）有几个节点（人）
    int max=0;
    for(int i=0;i<=n;i++){//人的编号从1~N
        if(num[i] > max)
            max=num[i];
    }
    cout<<max<<endl;
    return 0;
}

不知道我讲的明白了没，如果大家还没理解，可以看看这个博客，畅通工程并查集详解。