Gumbel distribution

目录

• 概
• 主要内容
  • 定义
  • Gumbel-Max trick
  • Gumbel trick 用于归一化
• 代码

概

感觉这个分布的含义很有用啊, 能预测‘最大', 也就是自然灾害, 太牛了.

主要内容

定义

[Gumbel distribution-wiki](Gumbel distribution - Wikipedia)

其分布函数和概率密度函数分别为:

\[F(x; \mu, \beta) = e^{-e^{-(x-\mu)/\beta}}, \quad f(x;\mu,\beta) = \frac{1}{\beta} e^{-[e^{-(x-\mu)/\beta}+(x-\mu) / \beta]}
\]

标准Gumbel分布(即\(\mu=0, \beta=1\)):

\[F(x) = e^{-e^{-x}}, \quad f(x) = e^{-(x+e^{-x})}.
\]

从Gumbel分布中采样, 只需:

\[x = F^{-1}(u) = \mu - \beta \ln (-\ln(u)), \quad u \sim \mathrm{Uniform}(0, 1).
\]

proof:

\[P(F^{-1}(u) \le x) = P(u \le F(x)) = F(x),
\]

故\(F^{-1}(u)\)的分布函数就是\(F(x)\).

\[\mathbb{E} [x] = \mu + \gamma \cdot \beta,
\]

其中 \(\gamma\)是Euler-Mascherorni constant.

Gumbel-Max trick

假设我们有一个离散的分布\([\pi_1, \pi_2, \cdots, \pi_k]\)共\(k\)类, \(\pi_i\)表示为第\(i\)类的概率, 则从该分布中采样\(z\)等价于

\[z = \arg \max_i [g_i + \log \pi_i], \quad g_i \sim \mathrm{Gumbel}(0, 1), \mathrm{i.i.d}.
\]

proof:

\[P(z=i) = P(g_i + \log \pi_i \ge \max \{g_j + \log \pi_j\}_{j\not=i}) = \int_{-\infty}^{+\infty} p(x) P(x+\log \pi_i \ge \{g_j + \log \pi_j\}_{j\not=i}) \mathrm{d}x.
\]

又

\[P(x+\log \pi_i \ge \{g_j + \log \pi_j\}_{j\not=i}) = \prod_{j\not=i} P(g_j \le x + \log\pi_i - \log \pi_j) = e^{-e^{-x} \cdot \frac{1 - \pi_i}{\pi_i}},
\]

带入计算得:

\[\begin{array}{ll}
P(z=i)
& = \int_{-\infty}^{+\infty} e^{-(x+e^{-x} \cdot \frac{1}{\pi_i})} \mathrm{d}x \\
& = \int_{-\infty}^{+\infty} \pi_i \cdot e^{-[(x-\log\frac{1}{\pi_i})+e^{-(x - \log \frac{1}{\pi_i})}]} \mathrm{d}x \\
& = \pi_i.
\end{array}
\]

Gumbel trick 用于归一化

我们时常会碰到这样的问题:

\[p(x;\theta) = \frac{f(x;\theta)}{Z},
\]

其中\(Z=\sum_{i=1}^K f(x_i;\theta)\) 是归一化常数, 那么怎么计算\(Z\)呢?

构建随机变量\(T\):

\[T = \max_i [\ln f(x_i) + g_i], \quad g_i \sim \mathrm{Gumbel}(-c, 1), \mathrm{i.i.d.}
\]

则

\[T \sim \mathrm{Gumbel}(-c + \ln Z)
\]

proof:

\[P(T \le t) = P(\max_i [\ln f(x_i) + g_i] \le t) = \prod_{i} P(g_i \le t - \ln f(x_i)) = e^{-e^{-(t+c-\ln Z)}} = F(t;-c+\ln Z ,1).
\]

因为

\[\mathbb{E}[T] = -c + \ln Z + \gamma,
\]

故我们只需估计\(\mathbb{E}[T] \approx \sum_j T_j\) 即可估计\(Z\)

\[Z = \exp (\sum_{j}T_j + c - \gamma).
\]

所以必须要求离散的\(x\)?

代码

[scipy-gumbel](scipy.stats.gumbel_r — SciPy v1.6.3 Reference Guide)

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gumbel_r

fig, ax = plt.subplots(1, 1)
# mean, var, skew, kurt = gumbel_r.stats(moments='mvsk')
# print(mean, var, skew, kurt)

x = np.linspace(gumbel_r.ppf(0.01), gumbel_r.ppf(0.99), 100)
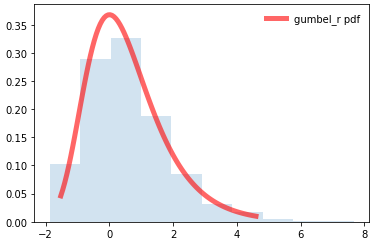
ax.plot(x, gumbel_r.pdf(x), 'r-', lw=5, alpha=0.6, label="gumbel_r pdf")
r = gumbel_r.rvs(size=1000, loc=0, scale=1)
ax.hist(r, density=True, histtype="stepfilled", alpha=0.2)
ax.legend(loc='best', frameon=False)
plt.show()