IMO 2021 第一题题解及相关拓展问题分析

IMO 2021 第 1 题：

设整数 n ≥ 100。伊凡把 n, n + 1, ..., 2n 的每个数写在不同的卡片上。然后他将这 n + 1 张卡片打乱顺序并分成两堆。证明：至少有一堆中包含两张卡片，使得这两张卡片上的数之和是一个完全平方数。

证：如果在 [n, 2n] 范围内存在 3 个整数 a、b、c，满足 a < b < c，且 a+b、a+c、b+c 都是完全平方数，则待证命题显然成立。考虑 a+b、a+c、b+c 是 3 个连续完全平方数的情形，由于 2 | a+b+a+c+b+c 知 居于中间位置的 a+c 必为偶数，令 a+c = (2k)² = 4k²，k 为正整数，则 a+b = (2k-1)²，b+c = (2k+1)²，进而有

a = 2k²-4k，b = 2k²+1，c = 2k²+4k    ①

由 a ≥ n 以及 c ≤ 2n，有 2(k-1)² ≥ n+2，2(k+1)² ≤ 2n+2，即有

1 + (n/2 + 1)^1/2 ≤ k ≤ (n+1)^1/2 - 1         ②

由 1 + (n/2 + 1)^1/2 ≤ (n+1)^1/2 - 1，可得出 n ≥ 48。但不能保证对每个大于等于 48 的 n 都有满足 ② 的 k 解，比如 n = 48，代入 ② 可得 k = 6，而 n = 49，则无 k 解。

为确保有 k 解，对 1 + (n/2 + 1)^1/2 + 1 ≤ (n+1)^1/2 - 1 求解，即

12(n+1)^1/2 <= n + 18

54² - 180 <= (n - 54)²     ③

当n ≥ 54·2 = 108 时，③ 显然成立。即当 n ≥ 108 时，命题成立。

当 n = 100 时，② 的左侧为 1 + (51)^1/2 ∈ (8,9)，右侧为 (101)^1/2 - 1 ∈ (9,10)，易知 k 取值只能为 9，代入 ① 有 a = 126, b = 163 ,c = 198

当 n = 101,...,107 时，易知 126、163、198 也都在 [n, 2n] 范围内。

综上，命题得证。

以下为拓展分析部分：

拓展问题一：把 n, n + 1, ..., 2n 这 n + 1 个整数（n > 2）无论怎样分成两组，其中总有至少一组中存在两个数之和是一个完全平方数，请判断在这 n + 1 个整数中是否一定存在 3 个整数 a、b、c，满足 a < b < c，且 a+b、a+c、b+c 都是完全平方数。

考察上面提到的 n = 49 时无 k 解的情形，在 49, 50, ..., 98 中取两数相加，易知其和的最小值和最大值分别为 99 和 195，而在 [99, 195] 范围内有 4 个完全平方数：100、121、144、169，处在三个连续完全平方数的中间且为偶数的只有 144 = (2·6)²，对应前述 k = 6 的情形，代入 ① 可得 a = 48, b = 73, c = 96。但是 48 不在 [49, 98] 之内，这说明，在 49, 50, ..., 98 中不存在 3 个整数 a、b、c，满足 a < b < c，且 a+b、a+c、b+c 都是完全平方数。

以下试图把 49, 50, ..., 98 分到 A、B 两组，使得两组中都不存在两个数之和为完全平方数，A、B 互为对应组。

49 + 51 = 100                   (I)

49→60 + 61←72 = 121    (II)

49→71 + 73←95 = 144    (III)

71→84 + 85←98 = 169    (IV)

把 49 放到 A 组，由 (I)、(II)、(III) 可知，51、72、95 都要放到 B 组，即

A: 49

B: 51, 72, 95

由 (II) 中的 51 + 70 = 121，以及 (III) 中的 51 + 93 = 144 可知，70、93 都要放到 A 组， 即

A: 49, 70, 93

B: 51, 72, 95

70 在 (III) 中，70 + 74 = 144，于是有

A: 49, 70, 93

B: 51, 72, 95, 74

72 在 (IV) 中，72 + 97 = 169，于是有

A: 49, 70, 93, 97

B: 51, 72, 95, 74

93 在 (IV) 中，76 + 93 = 169，于是有

A: 49, 70, 93, 97

B: 51, 72, 95, 74, 76

95 在(IV) 中，74 + 95 = 169，但是 74 和 95 已经在 B 组里了。

因此，由 n = 49 的情形分析可知，拓展问题一的答案是否定的。

对上述过程稍作提炼可知，49、51、70、74、95 这 5 个数由于 49+51、51+70、70+74、74+95、95+49 都是完全平方数，可形象地把这 5 个数（用更一般的 a、b、c、d、e 替代）排成五边形，则该五边形的每条边上的两数和（a+b、b+c、c+d、d+e、e+a）都是完全平方数。如下图所示：

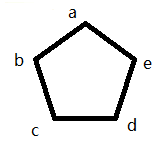
若把 a 放到 A 组，为避免 A 组中两数和为完全平方数，则与 a 相邻的 b 和 e 必需放到 B 组，同样 c 和 d 因为分别与 b 和 e 相邻，则必需放到 A 组，但 c 与 d 相邻，即无法保证 A、B 两组中都不出现两数和为完全平方数的情形。这个命题很容易扩展到任意奇数边形的一般情形：

对于任意 n 边形，n 为大于等于 3 的奇数，没有办法把 n 个顶点分配到两个集合 A 和 B，使得该 n 边形的任意一条边的两个顶点既不同在 A 也不同在 B。

由上面的分析，可以引入奇数环的概念：k 个不同正整数组成的 k 元组 (x₁, x₂, ..., x_k)，其中 k 为大于 1 的奇数，若该 k 元组中任意两个相邻数之和为完全平方数，且首尾两数之和（即 x₁ + x_k）也为完全平方数，则称这个 k 元组构成一个 k 阶奇数环，简称 k数环。

于是，原题的命题的等价说法就是：

若整数 n ≥ 100，则 n, n + 1, ..., 2n 中必定存在奇数环。

拓展问题一的结论用奇数环复述起来就很直观了，即：

若 n, n + 1, ..., 2n 中存在奇数环，则这个奇数环不一定是 3 数环。

拓展问题二：若从 n 个不同的正整数中任取两个相加，所能得到的和集里至多只有两个完全平方数。请问能否把这 n 个正整数分成两组使得每组中都不存在两数之和为完全平方数？

若和集中没有完全平方数，则问题的答案显然是肯定的。

考虑和集中只有一个完全平方数，记为 s，的情形。从这 n 个数中任取两个和为 s 的数，如 u + v = s，把 u 放入 A 组，把 v 放入 B 组。此时 A = {u}，B = {v}。剩余的数中如果还有两数之和为 s，如 p + q = s，同样把 p、q 分别放入 A 组和 B 组，此时 A = {u, p}，B = {v, q}。在 A 组中显然有 u + p ≠ s（不然 p = v，与题设矛盾）。依此类推，直到剩余的数中不再有两数之和为 s，则把这些数全部放入 A 组。易知此情形下，问题的答案同样是肯定的。

考虑和集中恰有两个完全平方数，分别记为 s₁ 和 s₂，的情形。从n 个数中寻找同时参与组建 s₁ 和 s₂ 的一个数，记为 u，即有 u + v = s₁，u + w = s₂，则把 u 放入 A 组，把 v 和 w 放入 B 组。此时 A = {u}，B = {v, w}，易知 v + w 既不等于 s₁，也不等于 s₂。把 v 和 w 加入待考察列表，依次考察列表中的数。以 v 为例：从列表中取出 v，如果未入组的数中有 x 使得 v + x = s₂，则把 x 放入 v 所在组的对应组，并把 x 加入待考察列表。继续考察列表中的数，直到列表为空。

重复上面的处理过程，直到待考察列表为空且未入组的数中不再有同时参与组建 s₁ 和 s₂ 的数。此时，未入组的数中若有 p + q = s₁（或 s₂），则把 p 放入 A 组，q 放入 B 组。重复这个过程，直到未入组的数中不再有参与组建 s₁ 或 s₂ 的数，最后把这些数全部放入 A 组。分组完成。易知此情形下，问题的答案同样是肯定的。

综上分析，拓展问题二的答案是肯定的。

扩展问题二的结论说明：任意一个奇数环所能组建的不同完全平方数的数目一定大于 2。

拓展问题三：

(I). 求 n 的最小值，使得 n, n + 1, ..., 2n 中存在奇数环；

(II). 求 k 的最小值，使得当 n ≥ k 时，n, n + 1, ..., 2n 中存在奇数环。

前述原题的证明过程，已经求得 n = 48 时，n, n + 1, ..., 2n 中存在奇数环。接下来要考察 n < 48 时，是否还有n, n + 1, ..., 2n 中存在奇数环。同样，由原题的结论，这里第二问里的 k 满足 k ≤ 100，接下来要进一步确定 k 的最小取值。

这两个问题通过编程来求解。在下一篇里提供。