Codeforces 549H. Degenerate Matrix 二分

二分绝对值,推断是否存在对应的矩阵

H. Degenerate Matrix

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

The determinant of a matrix 2 × 2 is defined as follows:

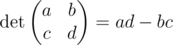
A matrix is called degenerate if its determinant is equal to zero.

The norm ||A|| of a matrix A is
defined as a maximum of absolute values of its elements.

You are given a matrix .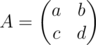
Consider any degenerate matrix B such that norm ||A - B|| is
minimum possible. Determine||A - B||.

Input

The first line contains two integers a and b (|a|, |b| ≤ 109),
the elements of the first row of matrix A.

The second line contains two integers c and d (|c|, |d| ≤ 109)
the elements of the second row of matrix A.

Output

Output a single real number, the minimum possible value of ||A - B||. Your answer is considered to be correct if its absolute
or relative error does not exceed 10 - 9.

Sample test(s)

input

1 2
3 4

output

0.2000000000

input

1 0
0 1

output

0.5000000000

Note

In the first sample matrix B is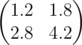 

In the second sample matrix B is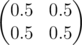 

import java.util.*;

public class Main
{
	double a,b,c,d;
	double[][] range = new double[4][2];

	double getMin(double L,double R,double l,double r)
	{
	   return Math.min(L*l,Math.min(L*r,Math.min(R*l,R*r)));
	}

	double getMax(double L,double R,double l,double r)
	{
	   return Math.max(L*l,Math.max(L*r,Math.max(R*l,R*r)));
	}

	boolean check(double e)
	{
		range[0][0]=a-e; range[0][1]=a+e; // x
		range[1][0]=b-e; range[1][1]=b+e; // y
		range[2][0]=c-e; range[2][1]=c+e; // z
		range[3][0]=d-e; range[3][1]=d+e; // w

		double A=getMin(range[0][0],range[0][1],range[3][0],range[3][1]);
		double B=getMax(range[0][0],range[0][1],range[3][0],range[3][1]);

		double C=getMin(range[1][0],range[1][1],range[2][0],range[2][1]);
		double D=getMax(range[1][0],range[1][1],range[2][0],range[2][1]);

		if((A>=C&&A<=D)||(B>=C&&B<=D)||(C>=A&&C<=B)||(D>=A&&D<=B)) return true;
		return false;

	}

	double Search()
	{
		double low=0.00000,high=100000000000.;
		int T_T=170;
		while(T_T-->0)
		{
			double mid=(low+high)/2.;
			if(check(mid)==true) high=mid;
			else low=mid;
		}
		return high;
	}

	Main()
	{
		Scanner in = new Scanner(System.in);

		a=in.nextDouble(); b=in.nextDouble();
		c=in.nextDouble(); d=in.nextDouble();

		System.out.printf("%.12f\n",Search());
	}

	public static void main(String[] args)
	{
		new Main();
	}
}