[ACM] POJ 2635 The Embarrassed Cryptographer （同余定理，素数打表）

The Embarrassed Cryptographer

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 11978		Accepted: 3194

Description

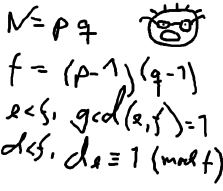The young and very promising cryptographer Odd Even has implemented the security module of a large system with thousands of users, which is now in use in his company. The cryptographic keys are
created from the product of two primes, and are believed to be secure because there is no known method for factoring such a product effectively. 

What Odd Even did not think of, was that both factors in a key should be large, not just their product. It is now possible that some of the users of the system have weak keys. In a desperate attempt not to be fired, Odd Even secretly goes through all the users
keys, to check if they are strong enough. He uses his very poweful Atari, and is especially careful when checking his boss' key.

Input

The input consists of no more than 20 test cases. Each test case is a line with the integers 4 <= K <= 10¹⁰⁰ and 2 <= L <= 10⁶. K is the key itself, a product of two primes. L is the wanted minimum size of the factors in the key. The input
set is terminated by a case where K = 0 and L = 0.

Output

For each number K, if one of its factors are strictly less than the required L, your program should output "BAD p", where p is the smallest factor in K. Otherwise, it should output "GOOD". Cases should be separated by a line-break.

Sample Input

143 10
143 20
667 20
667 30
2573 30
2573 40
0 0

Sample Output

GOOD
BAD 11
GOOD
BAD 23
GOOD
BAD 31

Source

field=source&key=Nordic+2005" style="text-decoration:none">Nordic 2005

解题思路：

给定两个数。一个数S是由两个素数 a,b相乘得到的数。还有一个数L随便，问 min(a,b) 是否小于L。

解题思路：素数打表，然后从前往后遍历看S能否被当前素数整除。假设整除，推断是否小于L。

注意：给定的S是大数。仅仅能用字符数组保存。

一个数a推断能不能整除b，仅仅要推断 a%b是否等于0就能够了。

同余定理：

(a+b)%c=(a%c+b%c)%c;

(a*b)%c=(a%c+b%c)%c;

对大数取余

模板：  大数字符串形式 a[1000];

char a[1000];

int m=0;

for(int i=0;a[i]!='\0';i++)

m=((m*10)%n+(a[i]-'0')%n)%n;//也能够写成  m=(m*10+a[i]-'0')%n

m为所求的余数

本题大数求余的方法为： 把字符串从后面起 三位三位的保存在一个int类型数组中，比方 12345   存在int类型数组里面为  12   345  然后依照前面的方法求：

bool mod(int n)
{
    int m=0;//气死我了！！

！

！！！

for(int i=0;i<=k-1;i++)
       m=(m*1000+num[i])%n;
    if(m==0)
        return true;
    return false;
}

做题时出了个BUG弄得头昏脑胀。半天后才发现原来int m=0; 一開始没有赋值为0.......哭死...

代码：

#include <iostream>
#include <stdio.h>
#include <string.h>
using namespace std;
const int maxn=1000005;
bool isprime[maxn+1];
int prime[maxn+1];
int primelen=0;//素数表的长度
int slen;//输入大数的长度
char s[10000];int l;
int num[600];int k;//转换后的长度

void sieve(int n)//筛法求素数
{
    for(int i=0;i<=n;i++)
        isprime[i]=1;
    isprime[0]=isprime[1]=0;
    for(int i=2;i<=n;i++)
    {
        if(isprime[i])
        {
            prime[primelen++]=i;
            for(int j=2*i;j<=n;j+=i)
                isprime[j]=0;
        }
    }
}

void change()//将字符串每三位（从后数）放在int数组中，比方 12345 ，  12   345
{
    k=0;
    int a=slen/3;
    int b=slen%3;
    int temp=0;
    if(b)//不能被3整除
    {
    for(int i=0;i<b;i++)
        temp=temp*10+s[i]-'0';
        num[k++]=temp;
    }
    int cnt=0;
    for(int i=1;i<=a;i++)
    {
        temp=0;
        int start=b+3*cnt;
        for(int j=0;j<3;j++)
            temp=temp*10+s[start+j]-'0';
        num[k++]=temp;
        cnt++;
    }
}

bool mod(int n)
{
    int m=0;//气死我了。！。！！！

for(int i=0;i<=k-1;i++)
       m=(m*1000+num[i])%n;
    if(m==0)
        return true;
    return false;
}

int main()
{
    sieve(maxn);
    while(cin>>s>>l&&(s[0]!='0'||l!=0))
    {
        slen=strlen(s);
        change();
        bool ok=1;
        int ans;
        for(int i=0;i<primelen;i++)
        {
            if(mod(prime[i])&&prime[i]<l)
            {
                ok=0;
                ans=prime[i];
                break;
            }
            if(prime[i]>=l)
                break;
        }
        if(ok)
            cout<<"GOOD"<<endl;
        else
            cout<<"BAD "<<ans<<endl;
    }
    return 0;
}