Maple trees（最小覆盖圆）

Maple trees

Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)

Total Submission(s): 222 Accepted Submission(s): 79

Problem Description

There are a lot of trees in HDU. Kiki want to surround all the trees with the minimal required length of the rope . As follow,

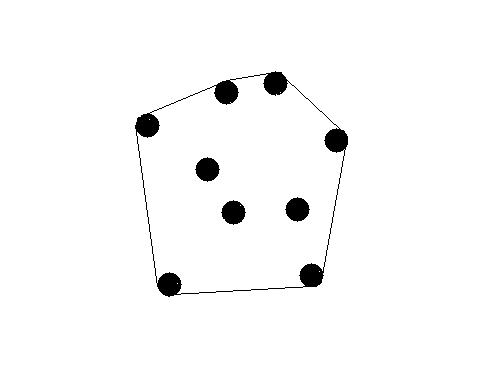To make this problem more simple, consider all the trees are circles in a plate. The diameter of all the trees are the same (the diameter of a tree is 1 unit). Kiki can calculate the minimal length of the rope , because it's so easy for this smart girl.
But we don't have a rope to surround the trees. Instead, we only have some circle rings of different radius. Now I want to know the minimal required radius of the circle ring. And I don't want to ask her this problem, because she is busy preparing for the examination.
As a smart ACMer, can you help me ?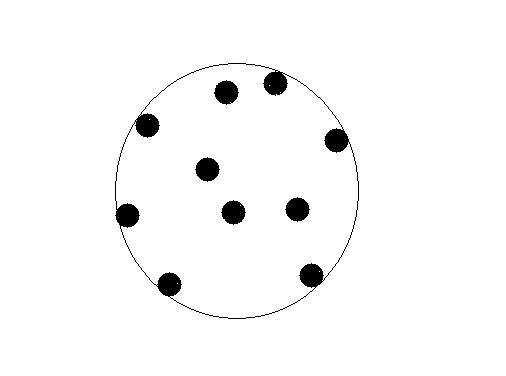

 

Input

The input contains one or more data sets. At first line of each input data set is number of trees in this data set n （1 <= n <= 100）, it is followed by n coordinates of the trees. Each coordinate is a pair of integers, and each integer is in [-1000, 1000], it means the position of a tree’s center. Each pair is separated by blank.
Zero at line for number of trees terminates the input for your program.

 

Output

Minimal required radius of the circle ring I have to choose. The precision should be 10^-2.

 

Sample Input

2
1 0
-1 0
0

 

Sample Output

1.50

 

Author

zjt

 

Recommend

lcy

 

/*
题意：给你散落的点，让你求出最小的圆，将这些点围起来，点可以在圆上，输出圆的最小半径。
 
初步思路：求出凸包，然后在求出这个凸包的外接圆，两条边的垂直平分线的交点就是圆心
 
#错误：有点天真，三角形一定有外接圆，但是多边形不一定有外接圆
 
#改进：求出凸包，然后求凸包的最小覆盖圆，这个名词也是看到博客才知道了（呜呜呜，又少了
       一次好好动脑的机会）然后任意的三个点组成的三角形的外接圆的最大半径就是就是凸包
       “外接圆”的半径了，三角形的外接圆半径为abc/4s，这个公式能简单的证明。遍历出所有的半径，中间最长的半径
       就是要求的半径。
#改进错误点：上面的情况只适用于锐角三角形，钝角，直角三角形的“外接圆”的最小半径，不是外接圆的半径，而是最长边的一半！
 
*/
#include<bits/stdc++.h>
using namespace std;
/****************************凸包模板*******************************/
const double eps = 1e-;
int sgn(double x)
{
    if(fabs(x) < eps)return ;
    if(x < )return -;
    else return ;
}
struct Point
{
    double x,y;
    Point(){}
    Point(double _x,double _y)
    {
        x = _x;y = _y;
    }
    Point operator -(const Point &b)const
    {
        return Point(x - b.x,y - b.y);
    }
    //叉积
    double operator ^(const Point &b)const
    {
        return x*b.y - y*b.x;
    }
    //点积
    double operator *(const Point &b)const
    {
        return x*b.x + y*b.y;
    }
    void input(){
        scanf("%lf%lf",&x,&y);
    }
};
struct Line {
    Point s,e;
    Line(){}
    Line(Point _s,Point _e) {
        s = _s; e = _e;
    }
};
//*两点间距离
double dist(Point a,Point b)
{
    return sqrt((a-b)*(a-b));
}
/*
* 求凸包，Graham算法
* 点的编号0~n-1
* 返回凸包结果Stack[0~top-1]为凸包的编号
*/
const int MAXN = ;
Point List[MAXN];
int Stack[MAXN];//用来存放凸包的点
int top;//表示凸包中点的个数
//相对于List[0]的极角排序
bool _cmp(Point p1,Point p2)
{
    double tmp = (p1-List[])^(p2-List[]);
    if(sgn(tmp) > )
        return true;
    else if(sgn(tmp) ==  && sgn(dist(p1,List[]) - dist(p2,List[])) <= )
        return true;
    else
        return false;
}
void Graham(int n)
{
    Point p0;
    int k = ;
    p0 = List[];
    //找最下边的一个点
    for(int i = ;i < n;i++)
    {
        if( (p0.y > List[i].y) || (p0.y == List[i].y && p0.x > List[i].x) )
        {
            p0 = List[i];
            k = i;
        }
    }
    swap(List[k],List[]);
    sort(List+,List+n,_cmp);
    if(n == )
    {
        top = ;
        Stack[] = ;
        return;
    }
    if(n == )
    {
        top = ;
        Stack[] = ;
        Stack[] = ;
        return ;
    }
    Stack[] = ;
    Stack[] = ;
    top = ;
    for(int i = ;i < n;i++)
    {
        while(top >  && sgn((List[Stack[top-]]-List[Stack[top-]])^(List[i]-List[Stack[top-]])) <= )
            top--;
        Stack[top++] = i;
    }
}
/****************************凸包模板*******************************/
int n;
int main(){
    // freopen("in.txt","r",stdin);
    while(scanf("%d",&n)!=EOF&&n){
        for(int i=;i<n;i++){
            List[i].input();
        }//输入所有点坐标
        if(n==){
            printf("0.50\n");
            continue;
        }
        if(n==){
            printf("%.2lf\n",dist(List[],List[])/+0.5);
            continue;
        }
        Graham(n);//求出凸包
        double Maxr=-1.0;
        // cout<<top<<endl;
        //将Static[0]作为所有小三角形的公共顶点
        for(int i=;i<top;i++){//枚举三角形的点
            for(int j=i+;j<top;j++){
                for(int k=j+;k<top;k++){
                    /*
                    三条边的长度
                    */
                    double a=dist(List[Stack[i]],List[Stack[j]]);
                    double b=dist(List[Stack[i]],List[Stack[k]]);
                    double c=dist(List[Stack[k]],List[Stack[j]]);
                    if(a*a+b*b<c*c||a*a+c*c<b*b||b*b+c*c<a*a){//判断是不是锐角三角形
                        Maxr=max(Maxr,max(max(a,b),c)/);
                    }else{
                        /*
                        三角形的面积
                        */
                        Point x1=List[Stack[j]]-List[Stack[i]];
                        Point x2=List[Stack[k]]-List[Stack[i]];
                        double s=fabs(x1^x2)/;
                        Maxr=max(Maxr,(a*b*c)/(*s));
                    }
                }
            }
        }
        printf("%.2lf\n",Maxr+0.5);
    }
    return ;
}