Support Vector Machines

支持向量机SVM。

简介

SVM核函数包括线性核函数、多项式核函数、径向基核函数、高斯核函数、幂指数核函数、拉普拉斯核函数、ANOVA核函数、二次有理核函数、多元二次核函数、逆多元二次核函数以及Sigmoid核函数。

支持向量机可能是最受欢迎的机器学习算法之一。

超平面是一个分割输入变量空间的线。在SVM中，选择一个超平面对输入变量空间中的点进行最优分类（类0或者类1，即二值分类）。

在二维中，你可以把它想象成一条直线，让我们假设所有的输入点都可以被这条线完全隔开。它是一种二类分类模型，其基本模型定义为特征空间上的间隔最大的线性分类器，其学习策略便是间隔最大化，最终可转化为一个凸二次规划问题的求解。

SVM学习算法发现了在超平面上最优分类的系数。

超平面与最近的数据点之间的距离称为边界。能够区分这两个类的最好或最优的超平面是有最大边界的直线。只有这些点与定义超平面和分类器的构造有关。这些点称为支持向量。他们支持或定义超平面。

在实践中，利用优化算法来寻找最大化边界的系数的值。

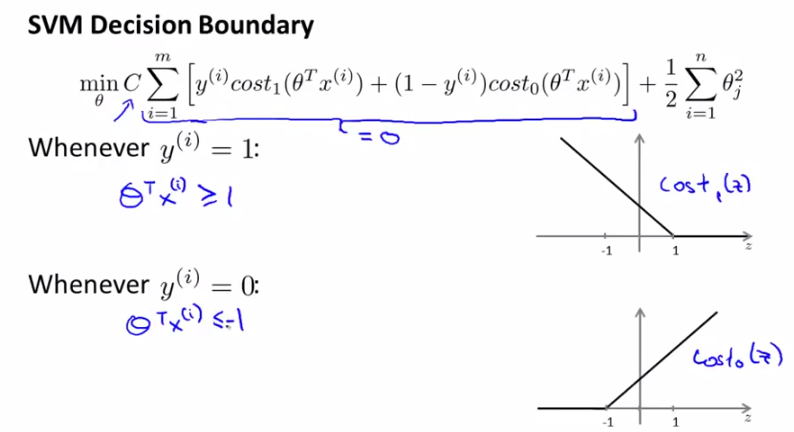
SVM可能是最强大的开箱即用的分类器之一，值得在您的数据集上尝试。

SVM的核心思想就是找到不同类别之间的分界面，使得两类样本尽量落在面的两边，而且离分界面尽量远。

最早的SVM是平面的，局限很大。但是利用核函数(kernel function)，我们可以把平面投射(mapping)成曲面，进而大大提高SVM的适用范围。

→

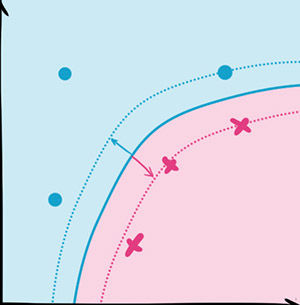
如右图，提高之后的SVM同样被大量使用，在实际分类中展现了很优秀的正确率。

适用情景

SVM在很多数据集上都有优秀的表现。

相对来说，SVM尽量保持与样本间距离的性质导致它抗攻击的能力更强。

和随机森林一样，这也是一个拿到数据就可以先尝试一下的算法。

优点：

1.可用于线性/非线性分类，也可以用于回归，泛化错误率低，计算开销不大，结果容易解释；

2.可以解决小样本情况下的机器学习问题，可以解决高维问题可以避免神经网络结构选择和局部极小点问题。

3.SVM是最好的现成的分类器，现成是指不加修改可直接使用。并且能够得到较低的错误率，SVM可以对训练集之外的数据点做很好的分类决策。

缺点：

1.对参数调节和和函数的选择敏感，原始分类器不加修改仅适用于处理二分类问题。

SVM和LR

首先，logistic regression（LR）的模型如下：

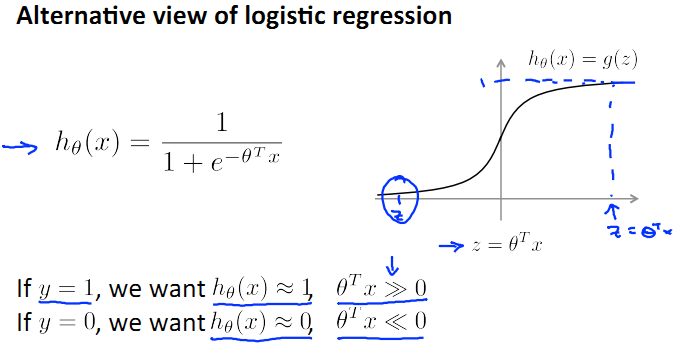
如下是SVM中cost function的定义。请看下图中玫瑰色的曲线，这就是我们希望得到的cost function曲线，和logistic regression的cost function非常相近，但是分为两部分。

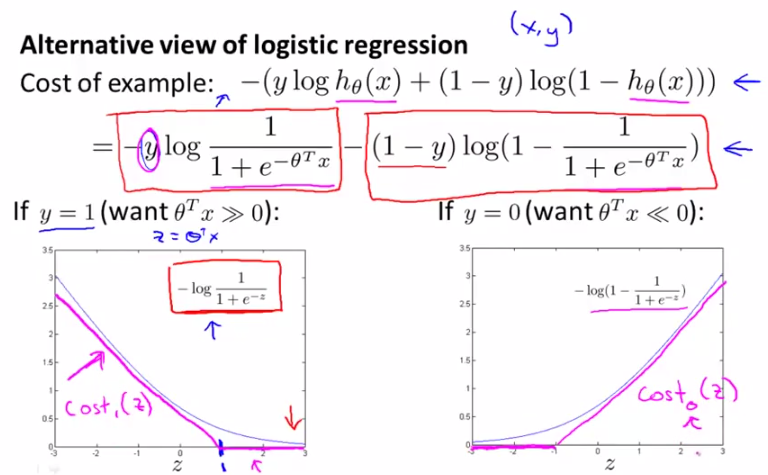
逻辑回归LR的cost function为：

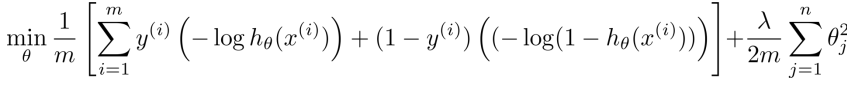
则SVM的cost function为：

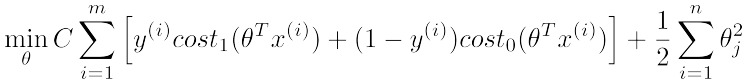
cost0和cost1分别对应y=0和y=1时的目标函数定义，最后一项regularization项和logistic regression中的类似。其实它们的最后一项本来是一样的，但是可以通过线性变换化简得到SVM的归一化项。

多分类扩展

SVM是针对二值分类问题提出的，并且成功地应用子解函数回归及一类分类问题·虽然支持向量机在解决二值分类问题时获得了巨大的成功，但实际应用中的大量多值分类问题也进一步要求如何将支持向量机推广到多分类问题上，目前有以下几种常用的方法：

一对多法。其思想是把某一种类别的样本当作一个类别，剩余其他类别的样本当作另一个类别，这样就变成了一个两分类问题。然后，在剩余的样本中重复上面的步骤`这种方法箱要构造k个svM模型，其中，k是待分类的个数。这种方案的缺点是训练样本数目大，训练困难。
一对一方法。其做法是在多值分类中，每次只考虑两类样本，即对每两类样本设计一个SVM模型，因此，总共需要设计 k(k一1)/2 个SVM模型.这种做法需要构造多个二值分类器，并且测试时需要对每两类都进行比较，导致算法计算复杂度很高。
SVM决策树法。它通常和二叉决策树结合起来，构成多类别的识别器。这种方法的缺点是如果在某个节点上发生了分类错误，将会把错误延续下去，该节点后续下一级节点上的分类就失去了意义。weston虽然提出了用一个优化式解多值分类问题’〕，但由于其变量t数目过多，所以只能在小型问题的求解中使用。一类分类方法的出现为异常值检测提供了一条新的思路，该方法通过核映射思想确定一个包含正类样本的紧致区域，以便使异常值更容易暴露出来，从而达到检测的目的。