切比雪夫定理（Chebyshev's theorem）与经验法则（Empirical Rule）
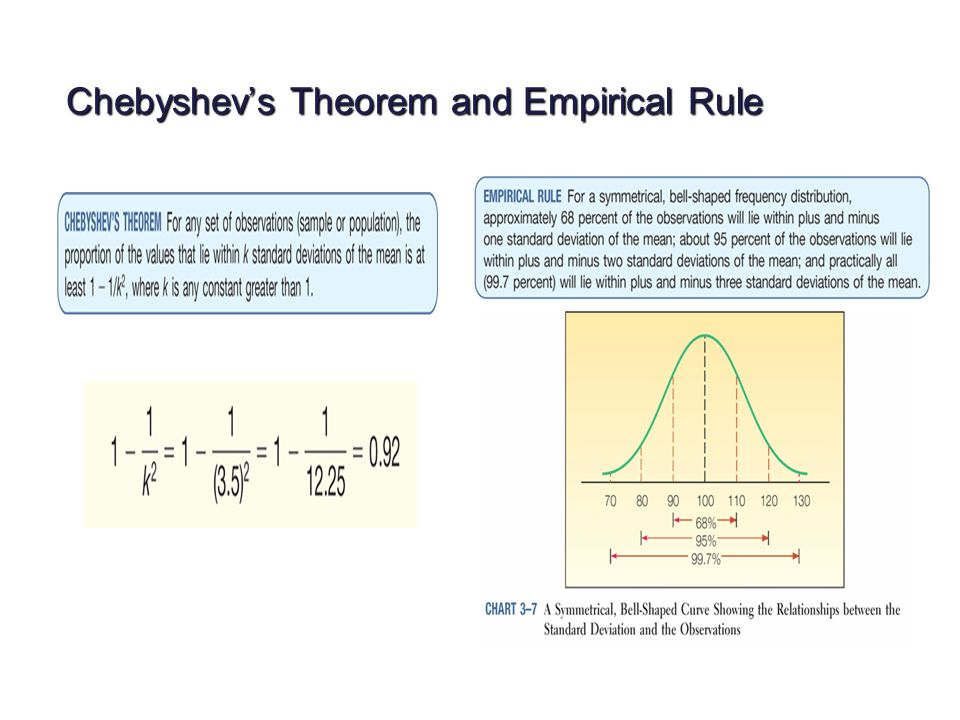
切比雪夫定理（Chebyshev's theorem）：适用于任何数据集，而不论数据的分布情况如何。
与平均数的距离在z个标准差之内的数值所占的比例至少为(1-1/z2)，其中z是大于1的任意实数。
至少75%的数据值与平均数的距离在z=2个标准差之内；
至少89%的数据值与平均数的距离在z=3个标准差之内；
至少94%的数据值与平均数的距离在z=4个标准差之内；
经验法则（Empirical Rule）：需要数据符合正态分布。
大约68%的数据值与平均数的距离在1个标准差之内；
大约95%的数据值与平均数的距离在2个标准差之内；
几乎所有的数据值与平均数的距离在3个标准差之内；
切比雪夫定理（Chebyshev's theorem）与经验法则（Empirical Rule）的更多相关文章
- 68.26-95.44-99.74 rule|empirical rule
6.3 Working with Normally Distributed Variables As illustrated in the previous example, the 68.26-95 ...
- 切比雪夫多项式(Chebyshev Polynomials)
切比雪夫多项式在逼近理论中有重要的应用.这是因为第一类切比雪夫多项式的根(被称为切比雪夫节点)可以用于多项式插值.相应的插值多项式能最大限度地降低龙格现象,并且提供多项式在连续函数的最佳一致逼近. 参 ...
- 主定理（Master Theorem）与时间复杂度
1. 问题 Karatsuba 大整数的快速乘积算法的运行时间(时间复杂度的递推关系式)为 T(n)=O(n)+4⋅T(n/2),求其最终的时间复杂度. 2. 主定理的内容 3. 分析 所以根据主定理 ...
- [笔记] 兰道定理 Landau's Theorem
兰道定理的内容: 一个竞赛图强连通的充要条件是:把它的所有顶点按照入度d从小到大排序,对于任意\(k\in [0,n-1]\)都不满足\(\sum_{i=0}^k d_i=\binom{k+1}{2} ...
- 斯托克斯定理（Stokes' theorem）
1. 几种形式 ∮∂SPdx+Qdy+Rdz=∬S∣∣∣∣∣∣cosα∂∂xPcosβ∂∂yQcosγ∂∂zR∣∣∣∣∣∣dS ∮∂Ωw=∬Ωdw 左边是内积: 右边是外积: 物理上的应用: ∮∂SE ...
- Ramsey's_theorem Friendship Theorem 友谊定理
w https://en.wikipedia.org/wiki/Ramsey's_theorem https://zh.wikipedia.org/wiki/拉姆齐定理 在组合数学上,拉姆齐(Rams ...
- （多项式）因式分解定理（Factor theorem）与多项式剩余定理（Polynomial remainder theorem）（多项式长除法）
(多项式的)因式分解定理(factor theorem)是多项式剩余定理的特殊情况,也就是余项为 0 的情形. 0. 多项式长除法(Polynomial long division) Polynomi ...
- 对主定理(Master Theorem)的理解
前言 虽说在学OI的时候学到了非常多的有递归结构的算法或方法,也很清楚他们的复杂度,但更多时候只是能够大概脑补这些方法为什么是这个复杂度,而从未从定理的角度去严格证明他们.因此借着这个机会把主定理整个 ...
- Law of large numbers and Central limit theorem
大数定律 Law of large numbers (LLN) 虽然名字是 Law,但其实是严格证明过的 Theorem weak law of large number (Khinchin's la ...
随机推荐
- 一个简单便捷的树形显示Ztree
这是本人在闲时研究的一个用于显示树形列表的小玩意. zTree 是一个依靠 jQuery 实现的多功能 “树插件”.优异的性能.灵活的配置.多种功能的组合是 zTree 最大优点. 下面就说说怎么用吧 ...
- js获取简单表单对象(1)
<form id="form"> <input type="text" name="username" value ...
- logback配置和使用
简介 logback是由log4j创始人设计的又一个开源日志组件.当前分成三个模块: logback-core是其它两个模块的基础模块. logback-classic是log4j的一个 改良版本.此 ...
- PyTorch 安装 报错，原因是pip 不是64位的。
原因: import pip._internal print(pip._internal.pep425tags.get_supported()) 换位64位的python版本. import pip. ...
- js学习之面向对象
一.创建对象的方法 1. {} 字面量创建 var person ={ name: "lisi", age: , say: function(){ alert(this.name) ...
- jquery如何监听浏览器窗口大小并根据不同的大小输出不同的值
$(window).bind("load resize",function(){ document.documentElement.clientWidth >= 600 ? ...
- python实现广度优先搜索
from collections import deque #解决从你的人际关系网中找到芒果销售商的问题#使用字典表示映射关系graph = {} graph["you"] = [ ...
- 升级.net core 3.x 后mvc项目调试状态编辑view代码不能实时预览
https://stackoverflow.com/a/58126955 简单来说 需要在nuget上安装Microsoft.AspNetCore.Mvc.Razor.RuntimeCompilati ...
- 一步一步从PostgreSQL安装到delphi 访问
今天,我们使用ubuntu 19 来安装PostgreSQL. 1.直接使用包安装 sudo apt-get install postgresql 按Y,直接安装. 安装完毕. 初次安装后,默认生成一 ...
- docker部署redis集群
一.查询最新redis镜像 docker search redis 二.下载redis镜像 docker pull redis 三.创建一个文件夹,以及创建redis-cluster.tmpl模板文件 ...