『保卫王国树上倍增dp』

<更新提示>

<正文>

保卫王国

Description

Z 国有n座城市，n - 1条双向道路，每条双向道路连接两座城市，且任意两座城市都能通过若干条道路相互到达。

Z 国的国防部长小 Z 要在城市中驻扎军队。驻扎军队需要满足如下几个条件：

一座城市可以驻扎一支军队，也可以不驻扎军队。

由道路直接连接的两座城市中至少要有一座城市驻扎军队。

在城市里驻扎军队会产生花费，在编号为i的城市中驻扎军队的花费是pipi。

小 Z 很快就规划出了一种驻扎军队的方案，使总花费最小。但是国王又给小 Z 提出了m个要求，每个要求规定了其中两座城市是否驻扎军队。小 Z 需要针对每个要求逐一给出回答。具体而言，如果国王提出的第j个要求能够满足上述驻扎条件（不需要考虑第 j 个要求之外的其它要求），则需要给出在此要求前提下驻扎军队的最小开销。如果国王提出的第j个要求无法满足，则需要输出-1 (1 ≤ j ≤ m)。现在请你来帮助小 Z。

Input Format

第 1 行包含两个正整数n,m和一个字符串type，分别表示城市数、要求数和数据类型。type是一个由大写字母 A，B 或 C 和一个数字 1，2，3 组成的字符串。它可以帮助你获得部分分。你可能不需要用到这个参数。这个参数的含义在【数据规模与约定】中有具体的描述。

第 2 行n个整数,pipi表示编号i的城市中驻扎军队的花费。

接下来 n - 1 行，每行两个正整数u,v，表示有一条u到v的双向道路。

接下来 m 行，第j行四个整数a,x,b,y(a ≠ b)，表示第j个要求是在城市a驻扎x支军队，在城市b驻扎y支军队。其中，x 、 y 的取值只有 0 或 1：若 x 为 0，表示城市 a 不得驻扎军队，若 x 为 1，表示城市 a 必须驻扎军队；若y为 0，表示城市 b不得驻扎军队，若y为 1，表示城市 b 必须驻扎军队。

输入文件中每一行相邻的两个数据之间均用一个空格分隔。

Output Format

输出共 m 行，每行包含 1 个整数，第j行表示在满足国王第j个要求时的最小开销，如果无法满足国王的第j个要求，则该行输出−1。

Sample Input

Sample Output

解析

如果不考虑特殊限制的话，就是一个最小权覆盖集问题，显然可以用树形$dp$做。

对于每一次限制都重做一遍$dp$显然是不行的，我们就要考虑怎样在预处理一些$dp$值的情况下快速求出被限制后的答案。没有任何限制的$dp$直接用"没有上司的舞会"一题的树上$dp$解法就可以了。

那么我们就需要考虑一次点对的限制会影响哪一些$dp$值，可以看下图：

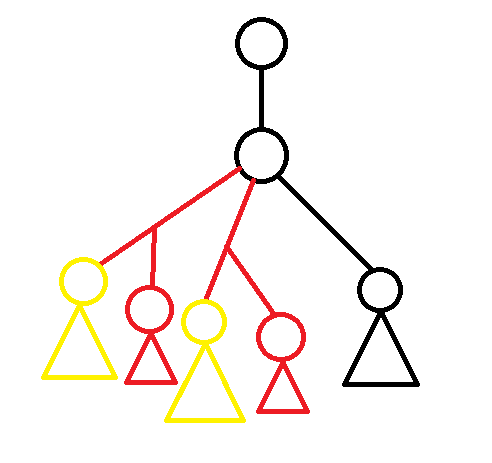
我们可以把限制后的树分为三部分，分别是图中的黑色，红色，黄色。黄色部分就是限制的两个点及其子树，红色的部分就是限制的两个点分别到其$lca$的路径和路径上的其它子树，黑色部分就是整棵树除了两个限制点$lca$的子树以为的部分。

我们发现黄色部分和黑色部分的$dp$值都是可以预处理的：

设$f[x][0/1]$代表以$x$为根的子树中，不取/取$x$这个点的最小权覆盖集

\[f[x][0]=\sum_{y\in son(x)} f[y][1]\\f[x][1]=\sum_{y\in son(x)}min(f[y][0],f[y][1])
\]

设$g[x][0/1]$代表除了以$x$为根的子树中，不取/取$x$这个点的最小权覆盖集

\[\forall y\in son(x)\ ,\ g[y][0]=g[x][1]+f[x][1]-min(f[y][0],f[y][1])\\ \forall y\in son(x)\ ,\ g[y][1]=min(g[y][0],g[x][0]+f[x][0]-f[y][1])
\]

好了，接下来就考虑红色部分怎么算了。处理树上点对到$lca$的路径问题，容易想到倍增求$lca$的遍历方式，又因为要处理路径上其他子树的$dp$值，所以我们可以设置一个如下的$dp$状态：

设$x$的$2^k$倍祖先的$p$，则$F[x][k][0/1][0/1]$代表$x$取/不取，$p$取/不取，$p$的子树减去$x$的子树这一部分的最小权覆盖集。

这是一个倍增的状态，于是就会有两个问题：如何预处理？如何拼接答案？

预处理的方式和普通的树上倍增差不多，重点看一下怎样倍增得到答案：

$1.$ 对于深度大一点的节点$x$，我们先把它跳到深度和$y$一样大的位置，并在倍增的过程中每次枚举两个端点取或不取的状态，用最小的花费转移即可，记录下答案。

$2.$ 用同样的方式将$x$，$y$两个点都向上跳，累加答案。

$3.$ 最后汇合到$lca$的两个儿子时，根据$lca$取或不取来讨论，得到两种答案，取最小值作为本次询问的答案。

其实，这道题本质上就是结合了树形$dp$和树上倍增两种算法，只要能够深入理解状态，就可以很快的想到倍增的方法。

$Code:$

#include<bits/stdc++.h>

using namespace std;

const int N = 100020 , M = 100020 , MaxlogN = 30;

const long long INF = 1LL<<60;

struct edge{int ver,next;}e[N*2];

int n,m,t,Head[N*2],val[N]; char op[10];

int dep[N],fa[N][MaxlogN+2];

long long f[N][2],g[N][2];

long long F[N][MaxlogN][2][2];

inline int read(void)

{

    int x = 0 , w = 0; char ch = ' ';

    while ( !isdigit(ch) ) w |= ch=='-' , ch = getchar();

    while ( isdigit(ch) ) x = x*10 + ch-48 , ch = getchar();

    return w ? -x : x;

}

inline void insert(int x,int y)

{

    e[++t] = (edge){y,Head[x]} , Head[x] = t;

    e[++t] = (edge){x,Head[y]} , Head[y] = t;

}

inline void input(void)

{

    n = read() , m = read();

    scanf("%s",op);

    for (int i=1;i<=n;i++)

        val[i] = read();

    for (int i=1;i<n;i++)

        insert( read() , read() );

}

// 先dfs求fa和dep,顺带求原始的dp数组f:子树x的最小权覆盖集

inline void dfs(int x,int Fa)

{

    dep[x] = dep[Fa] + 1 , fa[x][0] = Fa;

    f[x][1] = val[x];

    for (int i=Head[x];i;i=e[i].next)

    {

        int y = e[i].ver;

        if ( y == Fa ) continue;

        dfs( y , x );

        f[x][0] += f[y][1];

        f[x][1] += min( f[y][0] , f[y][1] );

    }

}

// 树形dp求g数组:子树x的补集的 最小权覆盖集

inline void dp(int x,int Fa)

{

    for (int i=Head[x];i;i=e[i].next)

    {

        int y = e[i].ver;

        if ( y == Fa ) continue;

        g[y][0] = g[x][1] + f[x][1] - min( f[y][0] , f[y][1] );

        g[y][1] = min( g[y][0] , g[x][0] + f[x][0] - f[y][1] );

        dp( y , x );

    }

}

// 利用f数组计算倍增数组

inline void prework(void)

{

    memset( F , 0x3f , sizeof F );

    for (int i=1;i<=n;i++)

    {

        int Fa = fa[i][0];

        F[i][0][0][0] = INF;

        F[i][0][0][1] = f[Fa][1] - min( f[i][0] , f[i][1] );

        F[i][0][1][0] = f[Fa][0] - f[i][1];

        F[i][0][1][1] = f[Fa][1] - min( f[i][0] , f[i][1] );

    }

    for (int k=1;k<=25;k++)

    {

        for (int i=1;i<=n;i++)

        {

            int Fa = fa[i][k-1];

            if ( !fa[Fa][k-1] ) continue;

            fa[i][k] = fa[Fa][k-1];

            for (int u=0;u<=1;u++)

                for (int v=0;v<=1;v++)

                    for (int w=0;w<=1;w++)

                        F[i][k][u][v] = min( F[i][k][u][v] , F[i][k-1][u][w] + F[Fa][k-1][w][v] );

        }

    }

}

// 树上倍增拼接答案

inline long long solve(int x,int a,int y,int b)

{

    if ( dep[x] < dep[y] )

        swap( x , y ) , swap( a , b );

    long long tx[2] = {INF,INF} , ty[2] = {INF,INF};

    long long nx[2],ny[2];

    tx[a] = f[x][a] , ty[b] = f[y][b];

    for (int i=25;i>=0;i--)

    {

        if ( dep[fa[x][i]] < dep[y] ) continue;

        nx[0] = nx[1] = INF;

        for (int u=0;u<=1;u++)

            for (int v=0;v<=1;v++)

                nx[u] = min( nx[u] , tx[v] + F[x][i][v][u] );

        tx[0] = nx[0] , tx[1] = nx[1];

        x = fa[x][i];

    }

    if ( x == y ) return nx[b] + g[y][b];

    for (int i=25;i>=0;i--)

    {

        if ( fa[x][i] == fa[y][i] ) continue;

        nx[0] = nx[1] = ny[0] = ny[1] = INF;

        for (int u=0;u<=1;u++)

            for (int v=0;v<=1;v++)

                nx[u] = min( nx[u] , tx[v] + F[x][i][v][u] ),

                ny[u] = min( ny[u] , ty[v] + F[y][i][v][u] );

        tx[0] = nx[0] , tx[1] = nx[1];

        ty[0] = ny[0] , ty[1] = ny[1];

        x = fa[x][i] , y = fa[y][i];

    }

    int p = fa[x][0];

    long long res1 = f[p][0] - f[x][1] - f[y][1] + tx[1] + ty[1] + g[p][0];

    long long res2 = f[p][1] - min( f[x][0] , f[x][1] ) - min( f[y][0] , f[y][1] )

                             + min( tx[0] , tx[1] ) + min( ty[0] , ty[1] ) + g[p][1];

    return min( res1 , res2 );

}

int main(void)

{

    input();

    dfs( 1 , 0 );

    dp( 1 , 0 );

    prework();

    for (int i=1;i<=m;i++)

    {

        int x = read() , a = read() , y = read() , b = read();

        if ( a == 0 && b == 0 && ( fa[x][0] == y || fa[y][0] == x ) )

            puts("-1");

        else printf("%lld\n",solve(x,a,y,b));

    }

    return 0;

}

<后记>