96. Unique Binary Search Trees

题目:

Given n, how many structurally unique BST's (binary search trees) that store values 1...n?

For example,
Given n = 3, there are a total of 5 unique BST's.

   1         3     3      2      1
    \       /     /      / \      \
     3     2     1      1   3      2
    /     /       \                 \
   2     1         2                 3

Hide Tags

Tree Dynamic Programming

Hide Similar Problems

(M) Unique Binary Search Trees II

 

链接： http://leetcode.com/problems/unique-binary-search-trees/

题解：

用DP求catalan number。  C_n+1 = ∑(C_{n - i} * C_i )， i 的范围是( 0 ~ n)。公式不太好写，改天要用Latex编辑一下。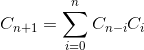。有机会的话也要好好学习一下解析组合数学 - Analytic Combinatorics。Sedgewick有本书专门讲这个。

Time Complexity - O(n)， Space Complexity - O(n)。

public class Solution {
    public int numTrees(int n) {        //catalan number
        if(n <= 0)
            return n;
        int[] dp = new int[n + 1];
        dp[0] = 1;    

        for(int i = 1; i < dp.length; i++) {
            for(int j = 0; j < i; j++) {
                dp[i] += dp[(i - 1) - j] *dp[j];
            }
        }

        return dp[n];
    }
}

或者用catalan数的另外一种推导，也是dp。

public class Solution {
    public int numTrees(int n) {     //Catalan number  Cn+1 = 2(2n + 1)/ (n+2) *  Cn
        if(n < 0)
            return 0;

        int[] count = new int[n + 1];
        count[0] = 1;

        for(int i = 1; i < n + 1;i++)
            count[i] = (int) (count[i - 1] * 2.0  *(2.0 *(i - 1) + 1.0) /(i - 1.0 + 2));

        return count[n];
    }
}

二刷:

求catalan number， 公式是C_n+1 = ∑(C_{n - i} * C_i )， 求和的范围是[0, n] 前后闭

Java:

public class Solution {
    public int numTrees(int n) {
        if (n <= 0) {
            return n;
        }
        int[] dp = new int[n + 1];
        dp[0] = 1;for (int i = 1; i <= n; i++) {
            for (int j = 0; j < i; j++) {
                dp[i] += dp[(i - 1) - j] * dp[j];
            }
        }
        return dp[n];
    }
}

三刷:

这里要仔细注意一下dp数组的创建以及计算公式时的边界条件。 我们求第n个数的结果的话，其实是wiki公式里的第n + 1个数。所以我们建立一个长度为n + 1的一维数组dp，最后返回dp[n]就可以了。 其中Catalan number公式仍然用的是公式是C_n+1 = ∑(C_{n - i} * C_i )， 求和的范围是[0, n] 前后闭。所以假如我们要求dp[i]， 那么内循环就是计算从0到 i-1 这 i 个数的乘积和。

Java:

Time Complexity - O(n)， Space Complexity - O(n)。

public class Solution {
    public int numTrees(int n) {
        if (n <= 0) return 1;
        int[] dp = new int[n + 1];
        dp[0] = 1;
        for (int i = 1; i <= n; i++) {
            for (int j = 0; j < i; j++) {
                dp[i] += dp[j] * dp[(i - 1) - j];
            }
        }
        return dp[n];
    }
}

题外话:

有空的话还是要学一学离散数学的各种知识。

Reference：

http://www.codecogs.com/latex/eqneditor.php

http://en.wikipedia.org/wiki/Catalan_number

http://mathworld.wolfram.com/BinaryTree.html