[HNOI2018]道路(DP)

题目描述

W 国的交通呈一棵树的形状。W 国一共有n−1n - 1n−1 个城市和nnn 个乡村，其中城市从111 到n−1n - 1n−1 编号，乡村从111 到nnn 编号，且111 号城市是首都。道路都是单向的，本题中我们只考虑从乡村通往首都的道路网络。对于每一个城市，恰有一条公路和一条铁路通向这座城市。对于城市i， 通向该城市的道路（公路或铁路）的起点，要么是一个乡村，要么是一个编号比iii 大的城市。 没有道路通向任何乡村。除了首都以外，从任何城市或乡村出发只有一条道路；首都没有往 外的道路。从任何乡村出发，沿着唯一往外的道路走，总可以到达首都。

W 国的国王小 W 获得了一笔资金，他决定用这笔资金来改善交通。由于资金有限，小 W 只能翻修n−1n - 1n−1 条道路。小 W 决定对每个城市翻修恰好一条通向它的道路，即从公路和铁 路中选择一条并进行翻修。小 W 希望从乡村通向城市可以尽可能地便利，于是根据人口调 查的数据，小 W 对每个乡村制定了三个参数，编号为iii 的乡村的三个参数是aia_iai​ ，bib_ibi​ 和cic_ici​ 。假设 从编号为iii 的乡村走到首都一共需要经过xxx 条未翻修的公路与yyy 条未翻修的铁路，那么该乡村 的不便利值为

ci⋅(ai+x)⋅(bi+y)c_i \cdot (a_i + x) \cdot (b_i + y)ci​⋅(ai​+x)⋅(bi​+y)

在给定的翻修方案下，每个乡村的不便利值相加的和为该翻修方案的不便利值。 翻修n−1n - 1n−1 条道路有很多方案，其中不便利值最小的方案称为最优翻修方案，小 W 自然 希望找到最优翻修方案，请你帮助他求出这个最优翻修方案的不便利值。

输入输出格式

输入格式：

第一行为正整数nnn 。

接下来n−1n - 1n−1 行，每行描述一个城市。其中第iii 行包含两个数si,tis_i,t_isi​,ti​ 。sis_isi​ 表示通向第iii 座城市 的公路的起点，tit_iti​ 表示通向第i座城市的铁路的起点。如果si>0s_i > 0si​>0 ，那么存在一条从第sis_isi​ 座城 市通往第iii 座城市的公路，否则存在一条从第−si-s_i−si​ 个乡村通往第i座城市的公路；tit_iti​ 类似地，如 果ti>0t_i > 0ti​>0 ，那么存在一条从第tit_iti​ 座城市通往第i座城市的铁路，否则存在一条从第−ti-t_i−ti​ 个乡村通 往第iii 座城市的铁路。

接下来nnn 行，每行描述一个乡村。其中第i行包含三个数ai,bi,cia_i,b_i,c_iai​,bi​,ci​ ，其意义如题面所示。

输出格式：

输出一行一个整数，表示最优翻修方案的不便利值。

输入输出样例

输入样例#1：复制

6
2 3
4 5
-1 -2
-3 -4
-5 -6
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

输出样例#1：复制

54

输入样例#2：复制

9
2 -2
3 -3
4 -4
5 -5
6 -6
7 -7
8 -8
-1 -9
1 60 1
1 60 1
1 60 1
1 60 1
1 60 1
1 60 1
1 60 1
1 60 1
1 60 1

输出样例#2：复制

548

输入样例#3：复制

12
2 4
5 3
-7 10
11 9
-1 6
8 7
-6 -10
-9 -4
-12 -5
-2 -3
-8 -11
53 26 491
24 58 190
17 37 356
15 51 997
30 19 398
3 45 27
52 55 838
16 18 931
58 24 212
43 25 198
54 15 172
34 5 524

输出样例#3：复制

5744902

说明

【样例解释 1】

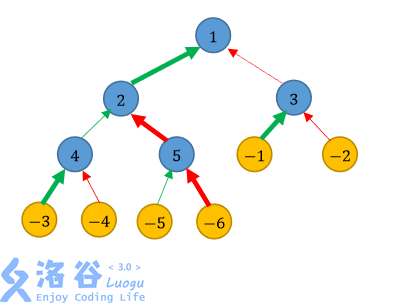
如图所示，我们分别用蓝色、黄色节点表示城市、乡村；用绿色、红色箭头分别表示 公路、铁路；用加粗箭头表示翻修的道路。

一种不便利值等于54的方法是：翻修通往城市2和城市5的铁路，以及通往其他城市的 公路。用→和⇒表示公路和铁路，用∗→和∗⇒表示翻修的公路和铁路，那么：

编号为1的乡村到达首都的路线为：-1 ∗→ 3 ⇒ 1，经过0条未翻修公路和1条未翻修铁 路，代价为3 × (1 + 0) × (2 + 1) = 9；
编号为2的乡村到达首都的路线为：-2 ⇒ 3 ⇒ 1，经过0条未翻修公路和2条未翻修铁 路，代价为2 × (1 + 0) × (3 + 2) = 10；
编号为3的乡村到达首都的路线为：-3 ∗→ 4 → 2 ∗→ 1，经过1条未翻修公路和0条未 翻修铁路，代价为3 × (2 + 1) × (1 + 0) = 9；
编号为4的乡村到达首都的路线为：-4 ⇒ 4 → 2 ∗→ 1，经过1条未翻修公路和1条未翻 修铁路，代价为1 × (2 + 1) × (3 + 1) = 12；
编号为5的乡村到达首都的路线为：-5 → 5 ∗⇒ 2 ∗→ 1，经过1条未翻修公路和0条未 翻修铁路，代价为2 × (3 + 1) × (1 + 0) = 8；
编号为6的乡村到达首都的路线为：-6 ∗⇒ 5 ∗⇒ 2 ∗→ 1，经过0条未翻修公路和0条未翻修铁路，代价为1 × (3 + 0) × (2 + 0) = 6；

总的不便利值为9 + 10 + 9 + 12 + 8 + 6 = 54。可以证明这是本数据的最优解。

【样例解释 2】

在这个样例中，显然应该翻修所有公路。

【数据范围】
一共20组数据，编号为1 ∼ 20。
对于编号≤4\le 4≤4 的数据，n≤20n \le 20n≤20 ；
对于编号为5 ∼ 8的数据，ai,bi,ci≤5a_i,b_i,c_i \le 5ai​,bi​,ci​≤5 ，n≤50n \le 50n≤50 ；
对于编号为9 ∼ 12的数据，n≤2000n \le 2000n≤2000 ；
对于所有的数据，n≤20000n \le 20000n≤20000 ，1≤ai,bi≤601 \le a_i,b_i \le 601≤ai​,bi​≤60 ，1≤ci≤1091 \le c_i \le 10^91≤ci​≤109 ，si,tis_i,t_isi​,ti​ 是[−n,−1]∪(i,n−1][-n,-1] \cup (i,n - 1][−n,−1]∪(i,n−1] 内的整数，任意乡村可以通过不超过40条道路到达首都。

本以为必有高论。

有个鬼啊！

普及DP入门题套一个废话极多的题面就往HNOI里出。

不想多说。

下面是考场程序，数据分治都没删，把数组范围改一下就A了，考场20，无语。

 #include<cstdio>
 #include<algorithm>
 #define rep(i,l,r) for (register int i=l; i<=r; i++)
 typedef long long ll;
 using namespace std;

 const int N=;
 const ll inf=;
 int n,x,y,fa[N],w[N],l1[N],l2[N],ch[N][],a[N],b[N],c[N];
 ll ans,f[N>>][][];

 void jud(){
     ll res=;
     rep(i,,n-){
         int x=,y=;
         for (int t=i+n; fa[t]; t=fa[t]){
             if (w[t]==) x++;
             if (w[t]==) y++;
         }
         res+=1ll*c[n+i]*(a[n+i]+x)*(b[n+i]+y);
     }
     ans=min(ans,res);
 }

 void dfs(int dq){
     if (dq==n) { jud(); return; }
     w[ch[dq][]]^=; dfs(dq+); w[ch[dq][]]^=;
     w[ch[dq][]]^=; dfs(dq+); w[ch[dq][]]^=;
 }

 void get(int x){
     if (!ch[x][]) return;
     l1[ch[x][]]=l1[x]+; l2[ch[x][]]=l2[x];
     l1[ch[x][]]=l1[x]; l2[ch[x][]]=l2[x]+;
     get(ch[x][]); get(ch[x][]);
 }

 ll get(int x,int i,int j){ return (ch[x][]) ? f[x][i][j] : 1ll*c[x]*(a[x]+i)*(b[x]+j); }

 void DP(int x){
     if (!ch[x][]) return;
     DP(ch[x][]); DP(ch[x][]);
     rep(i,,l1[x]) rep(j,,l2[x])
         f[x][i][j]=min(get(ch[x][],i,j)+get(ch[x][],i,j+),get(ch[x][],i+,j)+get(ch[x][],i,j));
 }

 int main(){
     freopen("road.in","r",stdin);
     freopen("road.out","w",stdout);
     scanf("%d",&n);
     if (n<=){
         rep(i,,n-){
             scanf("%d%d",&x,&y);
             if (x<=) x=-x+n-; if (y<=) y=-y+n-;
             ch[i][]=x; ch[i][]=y; fa[x]=fa[y]=i; w[x]=; w[y]=;
         }
         rep(i,,n-) scanf("%d%d%d",&a[n+i],&b[n+i],&c[n+i]);
         ans=inf; dfs(); printf("%lld\n",ans);
     }else{
         rep(i,,n-){
             scanf("%d%d",&x,&y);
             if (x<=) x=-x+n-; if (y<=) y=-y+n-;
             ch[i][]=x; ch[i][]=y; fa[x]=fa[y]=i; w[x]=; w[y]=;
         }
         rep(i,,n-) scanf("%d%d%d",&a[n+i],&b[n+i],&c[n+i]);
         get(); DP(); printf("%lld\n",f[][][]);
     }
     return ;
 }