2.1、Softmax Regression模型

Softmax Regression模型

　　由于Logistics Regression算法复杂度低，容易实现等特点，在工业中的到广泛的使用，但是Logistics Regression算法主要用于处理二分类问题，若需要处理的是多分类问题，如手写字的识别，即识别{0,1,2,3,4,5,6,7,8,9}中的数字，此时需要使用能够处理多分类问题的算法。

　　Softmax Regression算法是Logistics Regression算法在多分类问题上的推广，主要用于处理多分类问题，其中，任意两个类之间是线性可分的。

　　多分类问题，他的类标签y的取值个数大于2，如手写字识别，即识别{0,1,2,3,4,5,6,7,8,9}中的数字，手写字如图所示：

1、Softmax Regression算法模型用于解决多分类问题

　　Softmax Regression算法是Logistics Regression算法的推广，即类标签y的取值大于或等于2.假设有m个训练样本{（X^（1），y^（1）），（X^（2），y^（2）），........（X^（m），y^（m））}，对于Softmax Regression算法，其输入特征为X^（i）€Rⁿ⁺¹，类标签记为：y^（i）€{0,1，.......，k}。假设函数为每一个样本估计其所属的类别的概率P（y=j |X），具体假设函数为：

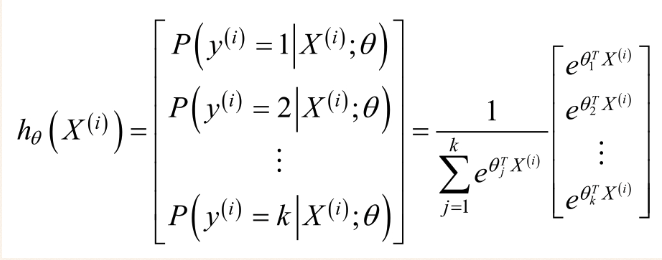
为了方便起见，我们同样使用符号θ来表示全部的模型参数。在实现softmax回归时，你通常会发现，将θ用一个k×(n+1)的矩阵来表示会十分便利，该矩阵是将θ_1,θ_2,...,θ_k按行罗列起来得到的，如下所示：

则对于每一个样本估计其所属的类别的概率为：

2、Softmax Regression算法的代价函数

　　类似于logistic Regression 算法，在Softmax Regression算法的损失函数中引入指示函数I（.），其具体形式为;

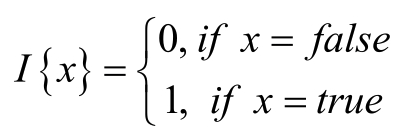
那么对于Softmax Regression算法的损失函数为;

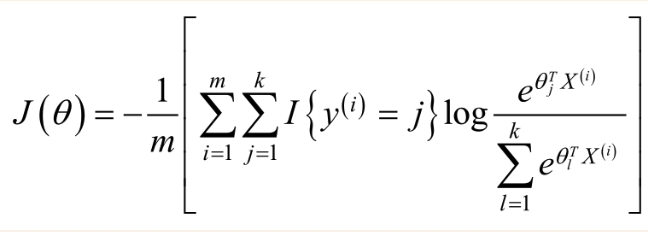
其中，I{y^（i）=j}表示的是当y^（i）属于第j类时，I{y（i）=j}=1，否则I{y^（i）=j}=0.

可以看出softmax是logistic的一个泛化版。logistic是k=2情况下的softmax回归。

3、Softmax Regression算法的求解

　　对于上述问题，可以使用梯度下降法对其进行求解，首先对其进行求梯度：

最终结果为：

注意，此处的θj表示的是一个向量，通过梯度下降法的公式更新：

现在，来使用Python实现上述Softmax Regression的更新过程

def gradientAscent(feature_data,label_data,k,maxCycle,alpha):
    '''利用梯度下降法训练Softmax模型
    :param feature_data: 特征
    :param label_data: 标签
    :param k: 类别个数
    :param maxCycle: 最大迭代次数
    :param alpha: 学习率
    :return weights: 权重
    '''
    m,n = np.shape(feature_data)
    weights = np.mat(np.ones((n,k)))#初始化权重
    i = 0
    while i<=maxCycle:
        err = np.exp(feature_data*weights)
        if i % 100 == 0:
            print("\t--------iter:",i,\
                  ",cost:",cost(err,label_data))
            rowsum = -err.sum(axis=1)
            rowsum = rowsum.repeat(k,axis = 1)
            err = err/rowsum
            for x in range(m):
                err[x,label_data[x,0]]+=1
            weights = weights+(alpha/m)*feature_data.T*err
            i+=1
        return  weights

cost函数：

 def cost(err,label_data):
     '''
     :param err: exp的值
     :param label_data: 标签的值
     :return: 损失函数的值
     '''
     m = np.shape(err)[0]
     sum_cost = 0.0
     for i in range(m):
         if err[i,label_data[i,0]]/np.sum(err[i,:])>0:
             sum_cost -=np.log(err[i,label_data[i,0]]/np.sum(err[i,:]))
         else:
             sum_cost -= 0
     return sum_cost / m

4、Softmax Regression与Logistics Regression的关系

有一点需要注意的是，按上述方法用softmax求得的参数并不是唯一的，因为，对每一个参数来说，若都减去一个相同的值，依然是上述的代价函数的值。证明如下：

　　

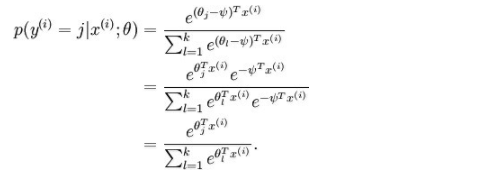
这表明了softmax回归中的参数是“冗余”的。更正式一点来说，我们的softmax模型被过度参数化了，这意味着对于任何我们用来与数据相拟合的估计值，都会存在多组参数集，它们能够生成完全相同的估值函数hθ将输入x映射到预测值。因此使J(θ)最小化的解不是唯一的。而Hessian矩阵是奇异的/不可逆的，这会直接导致Softmax的牛顿法实现版本出现数值计算的问题。

为了解决这个问题，加入一个权重衰减项到代价函数中：

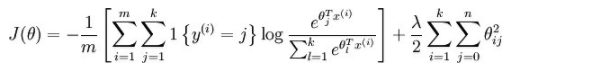
有了这个权重衰减项以后(对于任意的λ>0)，代价函数就变成了严格的凸函数而且hession矩阵就不会不可逆了。

此时的偏导数：

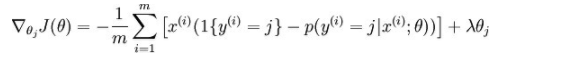
对于上面的Softmax Regression过度参数化问题可以参考博客：https://www.cnblogs.com/bzjia-blog/p/3366780.html