BZOJ2730 矿场搭建 解题报告 点双联通分量

题意概述：

　　一张有向图，在其中设置一些关键点（即题目中的逃生出口），使得删除任意一个点之后其余点都可以到达至少一个关键点。

　　问至少需要设置多少中关键点，有多少种设置方法。

解析：

　　首先，这道题要求删掉一个点，不难想到这道题与割点有关。其次，删掉一个点其他点仍然可以到达关键点就可以想到是点双联通分量。

　　但是，问题关键是，真的需要在每一个点双联通分量中都设置一个关键点吗？

　　

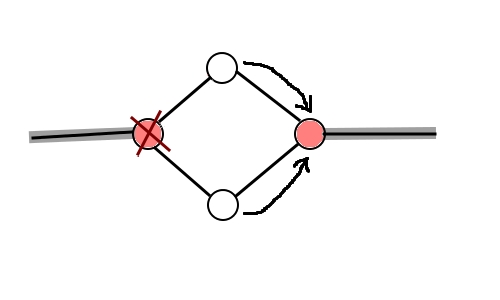
答案是否定的，因为如果一个双联通分量连接了两个或两个以上的割点，一个割点被删掉那么还可以通过另外的割点到达某个关键点，如上图，红色点为割点，灰底色的边为割边

所以只需统计含割点个数小于等于1的块数就是最少的关键点个数，如此，则放置关键点的方案数为各个被统计的块（割点数小于等于1的块）的点的个数的乘积，当然，若只找到了一个满足条件的块，那最少关键点数为2，方案数为（令n为点的个数）：  n*(n-1)/2.

需要注意的是这道题的数据规模：有500条边，但是并没有对点的编号的说明，所以点的标号可以是任意的，故此题建议离散化，但是我还是偷了个懒，因为数据中的点好像不超过50000

代码如下：

 #include <iostream>
 #include <algorithm>
 #include <cstdio>
 #include <cstring>
 #include <cstdlib>
 #include <cmath>
 #include <ctime>
 #include <vector>

 using namespace std;

 //#define    File
 //#define    Debug

 struct Edge
 {
     int    to;
     int    next;
 }e[];

 int    n,cnt,cnt_blocks,bcc_cnt,top,Ans,kase;
 int    p[],dfn[],nbcc[];

 long long    Sum;

 pair<int,int>    st[];
 vector<int>    bcc[];

 bool    cut[];

 inline    void    Add_edge(const int x,const int y)
 {
     e[++cnt].to=y;
     e[cnt].next=p[x];
     p[x]=cnt;
     return ;
 }

 int    Tarjan(const int S,const int fa)
 {
     int    child,lowu,lowv,v,i;

     dfn[S]=lowu=++cnt_blocks;
     child=;

     for(i=p[S];i;i=e[i].next)
     {
         v=e[i].to;
         if(!dfn[v])
         {
             st[++top]=make_pair(S,v);
             child++;
             lowv=Tarjan(v,S);
             lowu=min(lowv,lowu);
             if(lowv>=dfn[S])
             {
                 cut[S]=true;
                 bcc_cnt++;
                 bcc[bcc_cnt].clear();
                 while(true)
                 {
                     if(nbcc[st[top].first]!=bcc_cnt)
                     {
                         bcc[bcc_cnt].push_back(st[top].first);
                         nbcc[st[top].first]=bcc_cnt;
                     }
                     if(nbcc[st[top].second]!=bcc_cnt)
                     {
                         bcc[bcc_cnt].push_back(st[top].second);
                         nbcc[st[top].second]=bcc_cnt;
                     }

                     if(st[top].first==S && st[top].second==v)
                         {top--;break;}
                     top--;
                 }
             }
         }
         else if(dfn[v]<dfn[S]  && v!=fa)
         {
             st[++top]=make_pair(S,e[i].to);
             lowu=min(lowu,dfn[v]);
         }
     }

     if(fa< && child==)cut[S]=false;
     return lowu;
 }

 inline    void    Init()
 {
 /*int    n,cnt,cnt_blocks,bcc_cnt,top,Ans,kase;
 int    p[51000],dfn[51000],nbcc[51000];

 long long    Sum;

 pair<int,int>    st[51000];
 vector<int>    bcc[1100];

 bool    visited[51000],cut[51000];*/
     cnt=cnt_blocks=bcc_cnt=top=Ans=;
     Sum=;
     memset(p,,sizeof(p));
     memset(dfn,,sizeof(dfn));
     memset(nbcc,,sizeof(nbcc));
     memset(cut,,sizeof(cut));
     for(int i=;i<=;++i)
         bcc[i].clear();
     memset(st,,sizeof(st));
     return ;
 }

 int main()
 {
 #ifdef    File
     freopen("2730.in","r",stdin);
 #ifndef    Debug
     freopen("2730.out","w",stdout);
 #endif
 #endif

     int    i,j,x,y,cut_cnt;

     while(~scanf("%d",&n) && n)
     {
         Init();
         for(i=;i<=n;++i)
         {
             scanf("%d%d",&x,&y);
             Add_edge(x,y);
             Add_edge(y,x);
         }

         for(i=;i<=n;++i)
         {
             if(!dfn[i])Tarjan(i,-);
         }

         for(i=;i<=bcc_cnt;++i)
         {
             cut_cnt=;
             for(j=;j<(int)bcc[i].size();++j)
             {
                 if(cut[bcc[i][j]])cut_cnt++;
             }
             if(cut_cnt==)
             {
                 Ans++;
                 Sum*=(long long)(bcc[i].size()-cut_cnt);
             }
         }

         if(bcc_cnt==)
         {
             Ans=;
             Sum=bcc[].size()*(bcc[].size()-)/;
         }

         printf("Case %d: %d %lld\n",++kase,Ans,Sum);
     }

 #ifdef    File
     fclose(stdin);
 #ifndef    Debug
     fclose(stdout);
 #endif
 #endif

     return ;
 }