浅谈求lca

　　lca即最近公共祖先，求最近公共祖先的方法大概有3种，其实是窝只听说过3种，这3种做法分别是倍增求lca，树剖求lca和tarjan求lca，但是窝只会前2种，所以这里只说前2种算法了。

　　首先是倍增求lca，倍增求lca的思想是不断的向上跳，直到跳到lca为止

　

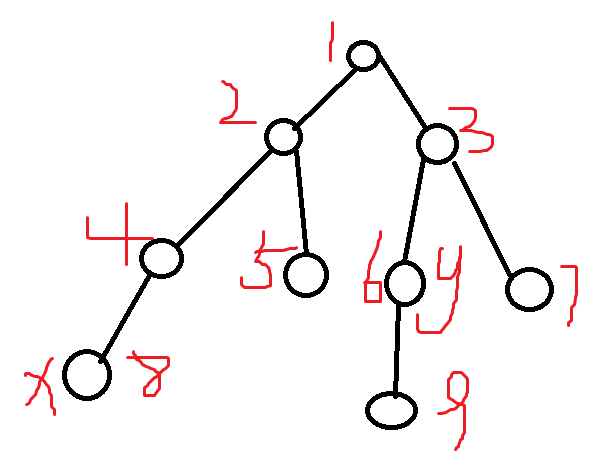
　　比如求这棵树中x和y的lca，首先让深度较深的点（x）跳到和深度较浅（y）的点同一个深度，然后先看一下x和y是不是同一个点了，如果是，那么不用再向上跳了，返回x即可。如果不是，需要继续往上跳，而这个往上跳的过程是判断如果跳到的那个深度x和y的祖先不是同一个就可以往上跳，因为如果是同一个的话很有可能跳过了，由于是这样跳的，所以最后x和y跳到的点是兄弟，这时只需要返回他们的父亲就好了。跳的过程相当于是对lca与x，y的深度差二进制分解，只不过不知道这个数是什么罢了。

模板：https://www.luogu.org/problemnew/show/P3379

代码：

 #include<iostream>
 #include<cstdio>
 using namespace std;
 const int maxn=;
 int n,m,s;
 int x,y;
 struct zhw{
     int to,last;
 }tu[maxn<<];
 int head[maxn],tot;
 void add(int x,int y)
 {
     tot++,tu[tot].last=head[x],head[x]=tot,tu[tot].to=y;
 }
 int fa[maxn][],deep[maxn];
 void dfs(int x)
 {
     for(int i=;i<=;++i)fa[x][i]=fa[fa[x][i-]][i-];
     for(int i=head[x];i;i=tu[i].last)
     {
         if(tu[i].to!=fa[x][])
         {
             fa[tu[i].to][]=x,deep[tu[i].to]=deep[x]+;
             dfs(tu[i].to);
         }
     }
 }
 int lca(int x,int y)
 {
     if(deep[x]<deep[y])swap(x,y);
     int t=deep[x]-deep[y];
     for(int i=;i>=;i--)
         if((<<i)&t)x=fa[x][i];
     if(x==y)return x;
     for(int i=;i>=;i--)
     {
         if(fa[x][i]!=fa[y][i])
             x=fa[x][i],y=fa[y][i];
     }
     return fa[x][];
 }
 int main()
 {
     scanf("%d%d%d",&n,&m,&s);
     for(int i=;i<n;++i)
     {
         scanf("%d%d",&x,&y);
         add(x,y),add(y,x);
     }
     deep[s]=;dfs(s);
     while(m--)
     {
         scanf("%d%d",&x,&y);
         printf("%d\n",lca(x,y));
     }
     return ;
 } 

　　树剖那个以后有空了在写QAQ