pagerank算法在数学模型中的运用（有向无环图中节点排序）

一.模型介绍

pagerank算法主要是根据网页中被链接数用来给网页进行重要性排名。

1.1模型解释

模型核心：

a. 如果多个网页指向某个网页A，则网页A的排名较高。

b. 如果排名高A的网页指向某个网页B，则网页B的排名也较高，即网页B的排名受指向其的网页的排名的影响。

名词解释：

（1）出链
如果在网页A中附加了网页B的超链接B-Link，用户浏览网页A时可以点击B-Link然后进入网页B。上面这种A附有B-Link这种情况表示A出链B。可知，网页A也可以出链C，如果A中也附件了网页C的超链接C-Link。

（2）入链
上面通过点击网页A中B-Link进入B，表示由A入链B。如果用户自己在浏览器输入栏输入网页B的URL，然后进入B，表示用户通过输入URL入链B

（3）无出链
如果网页A中没有附加其他网页的超链接，则表示A无出链

（4）只对自己出链
如果网页A中没有附件其他网页的超链接，而只有他自己的超链接A-Link，则表示A只对自己出链

（5）PR值
一个网页的PR值，概率上理解就是此网页被访问的概率，PR值越高其排名越高

网页存在的几种可能关系：

1.网页都有出入链

此种情况下的网页A的PR值计算公式为：

   A的PR值由B、C来决定，而B有两个出链，故为B的PR值的一半。

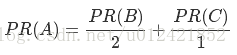
2.存在网页没有出链

网页C是没有出链。因为C没有出链，所以对A,B,D网页没有PR值的贡献。PageRank算法的策略：从数学上考虑，为了满足Markov链，设定C对A,B,C,D都有出链（也对他自己也出链~）。你也可以理解为：没有出链的网页，我们强制让他对所有的网页都有出链，即让他对所有网页都有PR值贡献。
此种情况PR(A)的计算公式：

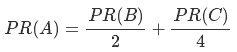C没有出链，则对所有的网页都有贡献，包括自己本身。

3.存在对自己出链的网页

C是只对自己出链的网页。
此时访问C时，不会傻乎乎的停留在C页面，一直点击C-Link循环进入C，即C网页只对自己的网页PR值有贡献。正常的做法是，进入C后，存在这种情况：在地址输入栏输入A/B/C/D的URL地址，然后跳转到A/B/C/D进行浏览，这就是PageRank算法解决这种情况的策略：设定存在一定概率为α，用户在地址栏输入A/B/C/D地址，然后从C跳转到A/B/C/D进行浏览。
此时PR(A)的计算公式为：

一般取值α=0.85

算法公式：

一般情况下，一个网页的PR值计算公式为：

注：Mpi是有出链到pi的所有网页集合，L(pj)是有网页pj的出链总数，N是网页总数，α一般取值为0.85

所有网页PR值同时计算需要迭代计算：一直迭代计算，停止直到下面2情况之一发生：每个网页的PR值前后误差dleta_pr小于自定义误差阈值，或者迭代次数超过了自定义的迭代次数阈值

二.实际案例

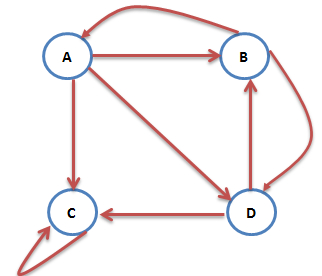
针对下图：

进行分析：

设定每个网站的PR值矩阵为PR，设定矩阵S为每个网站的出入链关系，S[i][j]表示网页j对网页i的出链，可知S[i]表示所有网页对网页i的出链值，S[:,j]是网页j对所有网页的出链值。

则上图的矩阵S为：

则由上分析，经过式子PR=α *S*PR+(1-α)/N，迭代达到结果PR趋于稳定时便可以停止迭代:

三.Python实现

# 输入为一个*.txt文件，例如
# A B
# B C
# B A
# ...表示前者指向后者

import numpy as np

if __name__ == '__main__':

    # 读入有向图，存储边
    f = open('input_1.txt', 'r')
    edges = [line.strip('\n').split(' ') for line in f]
    print(edges)

    # 根据边获取节点的集合
    nodes = []
    for edge in edges:
        if edge[0] not in nodes:
            nodes.append(edge[0])
        if edge[1] not in nodes:
            nodes.append(edge[1])
    print(nodes)

    N = len(nodes)

    # 将节点符号（字母），映射成阿拉伯数字，便于后面生成A矩阵/S矩阵
    i = 0
    node_to_num = {}
    for node in nodes:
        node_to_num[node] = i
        i += 1
    for edge in edges:
        edge[0] = node_to_num[edge[0]]
        edge[1] = node_to_num[edge[1]]
    print(edges)

    # 生成初步的S矩阵
    S = np.zeros([N, N])
    for edge in edges:
        S[edge[1], edge[0]] = 1
    print(S)

    # 计算比例：即一个网页对其他网页的PageRank值的贡献，即进行列的归一化处理
    for j in range(N):
        sum_of_col = sum(S[:,j])
        for i in range(N):
            S[i, j] /= sum_of_col
    print(S)

    # 计算矩阵A
    alpha = 0.85
    A = alpha*S + (1-alpha) / N * np.ones([N, N])
    print(A)

    # 生成初始的PageRank值，记录在P_n中，P_n和P_n1均用于迭代
    P_n = np.ones(N) / N
    P_n1 = np.zeros(N)

    e = 100000  # 误差初始化
    k = 0   # 记录迭代次数
    print('loop...')

    while e > 0.00000001:   # 开始迭代
        P_n1 = np.dot(A, P_n)   # 迭代公式
        e = P_n1-P_n
        e = max(map(abs, e))    # 计算误差
        P_n = P_n1
        k += 1
        print('iteration %s:'%str(k), P_n1)

    print('final result:', P_n)

读取文件为：

A B
A C
A D
B D
C E
D E
B E
E A

结果为：

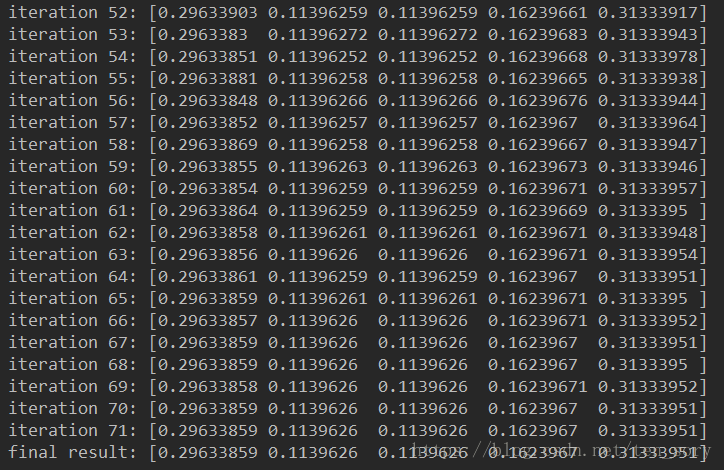
可视化代码：

import networkx as nx
import matplotlib.pyplot as plt

if __name__ == '__main__':

    # 读入有向图，存储边
    f = open('input_1.txt', 'r')
    edges = [line.strip('\n').split(' ') for line in f]

    G = nx.DiGraph()
    for edge in edges:
        G.add_edge(edge[0], edge[1])
    nx.draw(G, with_labels=True)
    plt.show()

结果如下：

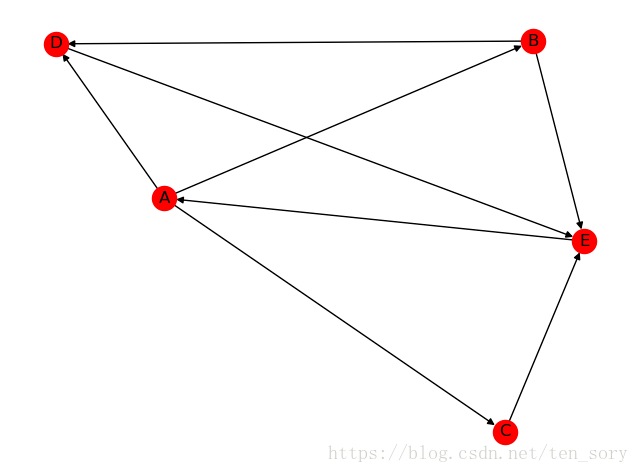
四.模型实战

题目如下：

背景：美国正在经历关于使用合成和非合成阿片类药物的国家危机，无论是治疗和管理疼痛（法律，处方用途）还是用于娱乐目的（非法，非处方用途）。美国疾病控制中心（CDC）等联邦组织正在努力“拯救生命并预防这种流行病对健康的负面影响，例如阿片类药物使用障碍，肝炎和艾滋病毒感染以及新生儿戒断综合症。”1简单地执行现行法律对于联邦调查局（FBI）和美国缉毒局（DEA）等来说，这是一项复杂的挑战。
对美国经济的重要部门也有影响。例如，如果阿片类药物危机扩散到美国人口的所有横截面（包括受过大学教育的人和具有高级学位的人），那么企业需要精确的劳动技能，高技术组件装配以及与客户的敏感信任或安全关系。客户可能难以填补这些职位。此外，如果老年人中阿片类药物成瘾的比例增加，医疗保健费用和辅助生活设施的人员配置也将受到影响。
DEA /国家法医实验室信息系统（NFLIS）作为缉毒局（DEA）转移控制办公室的一部分，发布了一份数据密集的年度报告，涉及“联邦，州分析的药物鉴定结果和相关信息”和当地的法医实验室。“ NFLIS内的数据库包括来自犯罪实验室的数据，这些数据处理了该国估计每年120万州和地方毒品案件的88％。对于这个问题，我们关注位于美国五（5）个州的个别县：俄亥俄州，肯塔基州，西弗吉尼亚州，弗吉尼亚州和田纳西州。在美国，一个县是每个拥有税收权力的州下面的下一级政府。提供此问题描述的是几个供您使用的数据集。第一份文件（MCM_NFLIS_Data.xlsx）包含2010-2017年麻醉镇痛药（合成阿片类药物）和海洛因的药物鉴定计数，这些药物来自这五个州的每个县，由各州的犯罪实验室向DEA报告。当执法机构向犯罪实验室提交证据作为刑事调查的一部分并且实验室的法医科学家对证据进行检验时，就会发生药物鉴定。通常，当执法机构提交这些样本时，他们会提供位置数据（县）及其事故报告。当证据提交给犯罪实验室并且未提供此位置数据时，犯罪实验室使用提交案件的市/县/州调查执法组织的位置。出于此问题的目的，您可以假设县位置数据是正确的。其他七（7）个文件是压缩文件夹，其中包含美国人口普查局的摘录，这些摘录代表了2010-2016每年中为这五个州的县收集的一组共同的社会经济因素（ACS_xx_5YR_DP02.zip）。 （注：2017年没有相同的数据。）
每个数据集都有一个代码表，用于定义所记录的每个变量。虽然您可以使用其他资源进行研究和背景信息，但提供的数据集包含您应该使用的唯一数据来解决此问题。

问题：
第1部分。使用提供的NFLIS数据，建立一个数学模型来描述五个州及其县之间和之间报告的合成阿片类药物和海洛因事件（病例）的传播和特征。使用您的模型，确定在五种状态中每种状态下可能已开始使用特定阿片类药物的任何可能位置。如果您的团队确定的模式和特征继续存在，那么美国是否存在任何具体问题。
政府应该有？在这些药物识别阈值水平发生这些情况？您的模型何时何地预测它们将来会发生？
第2部分。使用美国人口普查提供的社会经济数据，解决以下问题：
有许多相互竞争的假设被提供作为阿片类药物使用如何达到目前水平的解释，使用/滥用阿片类药物，促使阿片类药物使用和成瘾增长的原因，以及为什么阿片类药物的使用仍然存在已知的危险。是否使用或使用趋势与提供的任何美国人口普查社会经济数据有关？如果是这样，请从第1部分修改模型以包含此数据集中的任何重要因素。第3部分。最后，结合您的第1部分和第2部分结果，确定可能的对抗阿片类药物危机的策略。使用您的模型来测试该策略的有效性;识别成功（或失败）所依赖的任何重要参数界限。除了主要报告之外，还要向首席管理员提供1-2页的备忘录，DEA / NFLIS数据库，总结您在此建模过程中发现的任何重要见解或结果。

解决标注黄色部分的问题，预测在何处会发生阿片和海洛因类药物的出现。