MATLAB矩阵运算

1. 矩阵的加减乘除和(共轭)转置

(1) 矩阵的加法和减法

　　如果矩阵A和B有相同的维度(行数和列数都相等)，则可以定义它们的和A+B以及它们的差A-B，得到一个与A和B同维度的矩阵C，其中C_ij=A_ij+B_ij或A_ij-B_ij.

另外Matlab还支持任意一个矩阵A与一个标量s相加，结果为矩阵的每一个元素加减标量，得到一个与A同维度的新的矩阵，即A+s的各个元素为A_ij+s.

(2) 矩阵的乘法

　　如果矩阵A的列数等于矩阵B的行数，则可以将A和B相乘，命令为A*B，得到一个新的矩阵C，C的行数等于A的行数，列数等于B的列数. 由于矩阵的乘法不满足交换律，所以一般A*B不等于B*A.

(3) 矩阵的张量积（tensor product）

　　矩阵A和B的张量积A⊗B可以方便地用kron函数计算，即使用命令kron(A,B), 例如

(4) 矩阵的除法

　　在MatLab中，有两个矩阵除法符号，左除\和右除/. 如果A是一个非奇异方阵(nonsingular square, 即满秩方阵)，B的行数与A的行数相等，那么A\B=A^-1B. 如果C的列数与A的列数相等，那么C/A=CA^-1.

　　从另一个角度来看，X=A\B是矩阵方程AX=B的解，X=C/A是矩阵方程XA=C的解. 如果b是一个行数与A的行数相等的列向量，则向量x=A\b是线性方程组 Ax=b的解. 且在矩阵方程AX=B中，A可以是一个m×n的矩阵，如果m=n则有唯一解；如果m<n则有多个解，Matlab会返回一个基础解；如果m>n则会返回一个最小方阵解.

(5) 矩阵的转置和共轭转置

　　在Matlab中，矩阵的共轭转置用撇号’表示，如果不需要对元素进行共轭运算，仅仅只对矩阵进行转置，则在撇号之前输入一个点号，即 .’ . 对于实数矩阵A，A’和A.’是相同的.

2. 矩阵元素操作运算

　　矩阵的运算既可以是如前所述的正常的整体运算，也可以是矩阵对应的元素依次进行标量运算，也叫数组运算，即把矩阵看做是二维数组. 对矩阵进行数组运算后得到的结果是一个与参与运算的矩阵维度相同的新矩阵，.这种元素间的算术运算的前提是参与运算的两个矩阵的维数要相同.

对于加法和减法，元素操作运算和矩阵运算没有差别，而对于乘、除和幂运算符，相应的数组运算符是在一般的算术运算符前面加上一个点号，如

+       -       .*       ./       .\       .^

其中，A./B 是指A中的元素除以B中相应的元素，即A./B 的第i行第j列的元素(A./B)_ij=A_ij/B_ij，而(A.\B)_ij=B_ij\A_ij. 这些元素运算符的使用例子如下所示：

　　

　　

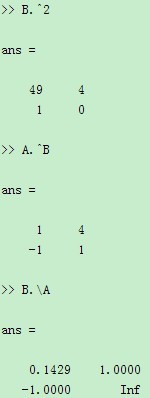
　　在Matlab中预定义的数学标准函数，如sin(x), abs(x)等都是基于对矩阵元素的运算. 如果函数f(x)是这样的一个函数，A是一个m×n的矩阵，其元素是a_ij ,那么 f(A)也是一个m×n的矩阵，其第i行第j列的元素为f(a_ij)，例如

　　

其中pi是Matlab的预定义变量，值为π，i也是预定义变量，表示复数的单位.

3. 常用的矩阵函数

　　矩阵函数是指参数为矩阵的函数，函数结果可能是一个标量值也可能是一个函数或者向量. Matlab中常用的矩阵函数包括：

　　(1) rank(A): 求矩阵A的秩，即A中线性无关的行数或者线性无关的列数.

　　

　　(2) det(A): 求矩阵A的行列式值.

　　

　　(3) inv(A): 如果A是一个非奇异(nonsingular)矩阵，则inv(A)返回A的逆矩阵. 另外还可以用左除A\eye(n)或右除eye(n)/A来计算A的逆，且在Matlab中用左除或右除来计算逆所花的计算时间比用inv函数要少，也比inv具有更好的容错性(error-detection properties).

　　(4) dot(x,y): 求同维度的向量x和y的内积/点积. 若A和B是两个具有相同维度的矩阵，则dot(A,B)是计算A和B对应列的内积，结果是一个行向量，这个行向量的列数等于A或B的列数. 例如

　　

　　(5) cross(x,y): 计算同维度的向量x和y的叉积，结果是一个向量，其方向由右手定则决定，长度等于|x|*|y|sin<x,y>. 若A和B是两个具有相同维度的矩阵，则cross(A,B)是计算A和B对应列的叉积，结果是一个维度与A和B相等的矩阵.

　　(6) kron(A,B): 得到矩阵A和B的张量积.

　　(7) isequal(A,B): 如果矩阵A和B是相同的，即具有相同的维数和相同的内容，则返回1.

　　(8) isreal(A): 判断A是否是一个实矩阵，如果是则返回1，否则返回0.

　　(9) trace(A): 计算方阵A的迹，即对角线元素之和.

　　(10) eig(A): 计算方阵A的特征值，结果是一个列向量，向量中元素的个数等于特征值的个数，即A的维度(A的行数或列数).

　　(11) [U,D]=eig(A): 计算方阵A的特征值和特征向量，得到两个方阵U和D，其中D的对角线元素为A的特征值，U的列向量为A的特征向量(可能是未normalize的结果)，例如