Trie树的二三事QWQ

写在前面

Trie，又称字典树，是一种用于实现字符串快速检索的多叉树结构。Trie的每个结点都拥有若干字符指针，若在插入或检索字符串时扫描到一个字符c，就沿着当前节点的c这个字符指针，走向该指针指向的结点。

我的没有指针的版本理解：树上的每个结点都记录了两个信息，一是这个结点所代表的字符，二是这个字符是否是一个字符串的结尾

---

正文：Trie树的基本操作

一、建立一棵Trie树

1.初始化

一棵空Trie树仅包含一个根结点，这个根结点不代表任何字符

2.插入

当需要插入一个字符串S时，我们从根结点开始，扫描当前树上结点的所有子结点，同时与字符串中当前这一位的字符匹配，于是就可能出现两种情况：

<1>匹配成功，当前树上的这个结点恰好有一个子结点代表的是字符串中当前这一位的字符，则直接开始扫描这个子结点的所有子结点，去匹配字符串中的下一位字符

<2>匹配失败，那么我们就给树上的这个结点增加一个子结点代表字符串中当前这一位的字符，然后继续进程

要注意的一点是，如果当前的这个字符是字符串中的最后一位，那么就要在树上的相应结点处记录一下。

这样干讲484有点难懂？让我来举个栗子吧QAQ

假设我现在要插入的字符串是stark(没错我就是漫威死忠粉还有我本来想插一个Marvel的但是太长了)

目前的Trie数是酱紫的

然后我现在要开始往里插入啦！当前状态是扫描到树上的根结点&字符串的第1位

如上所述我现在要在根结点的子结点中查找代表了字符“s”的结点

转化成图就是酱紫哒

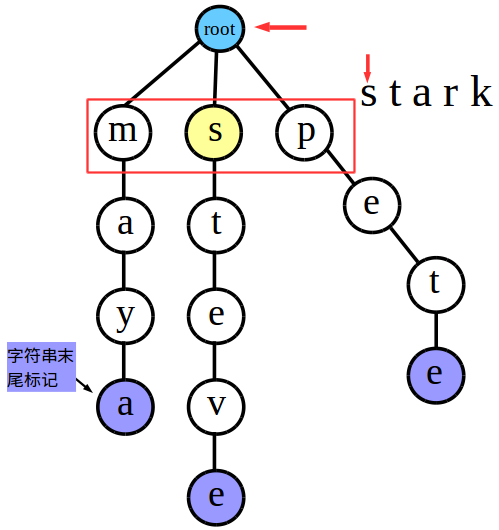
此时就是我说道的第<1>种情况，我们发现根结点的子结点中恰好有一个结点可以与字符串中的这一位匹配，于是我们继续操作……

同样的，“t”也可以匹配，那我们就继续往下走……

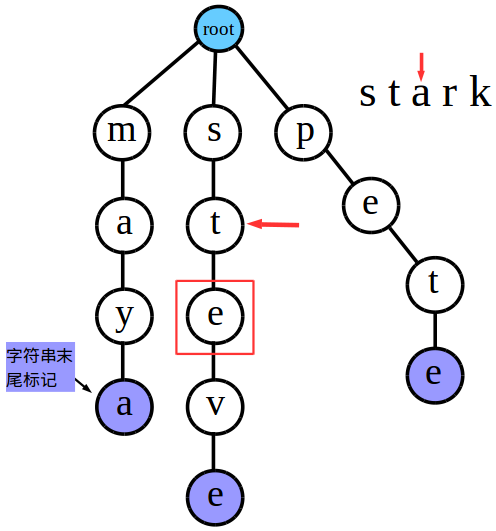
现在扫描到代表t的结点，发现它的子结点中没有能和字符串中当前这一位“a”相匹配的，于是我们就给代表t的结点插入一个子结点代表a

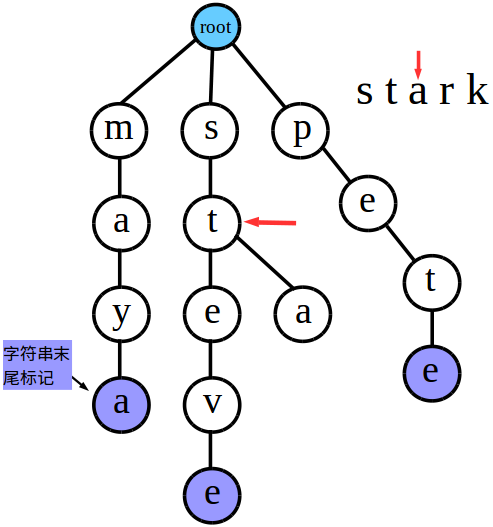
就是酱紫啦！然后我们再继续往下操作……

中间过程我就省略啦，重复之前的步骤就好QWQ

一个世纪之后……我们的Trie树就变成了这个样子

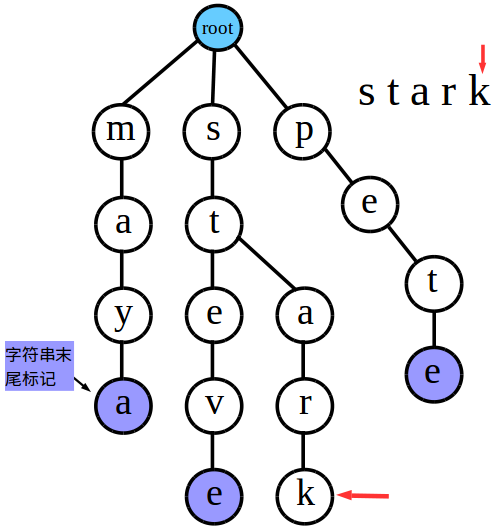
最后别忘了在代表字符串结尾字符的结点打上标记哦

好啦，到此为止，我们就完成了向Trie树中插入一个字符串的操作啦！^_^

3.代码实现

struct T{
    bool end;//是否为字符串结尾
    int son[];
//表示子结点中此种字符的编号(存在位置)，这里假设是26个小写字母
    char ch;//当前结点所代表的字符(其实这个可以不要QAQ)
}Trie[max_point];//max_point为最大结点数目
void build(string s){//s是要插入Trie树的字符串
    int len=s.length();
    int now=;
    for(int i=;i<len;i++){
        if(!Trie[now].son[s[i]-'a']){//如果子结点中不存在这个字符
            Trie[now].son[s[i]-'a']=++num;//num记录总结点数
            Trie[num].ch=s[i];
        }//构建出这个结点
        now=Trie[now].son[s[i]-'a'];//继续访问
    }
    Trie[now].end=;//标记字符串结尾
}

应该是对的吧，我也没有试过呀QAQ(瑟瑟发抖的蒟蒻)

---

二、在Trie树上进行检索

当需要检索一个字符串S在Trie中是否存在时，我们可以像插入操作一样去扫描。

检索的结果无非就是存在和不存在两种情况

存在很简单，而对于不存在，同样会有两种情况

1.在匹配字符串中的字符和Trie树上的结点时，出现Trie树上不存在代表字符串中的某一个字符的情况，那么显然这个字符串就不可能存在于Trie树中了

2.匹配时字符串中的每一个字符都按顺序存在与Trie树中，但Trie树中代表字符串中最后一个字符的结点没有被标记为字符串结尾，那么这个字符串同样也是不存在于Trie树中的

就拿我们刚刚建立的Trie树举个栗子吧

现在我要检索三个字符串是否存在于Trie树中

这三个字符串分别是“maya”“soldier”“pet”(字符串不包括“”)

我们先来检索“maya”

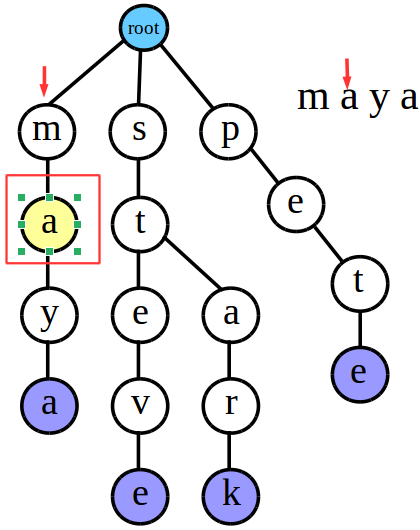
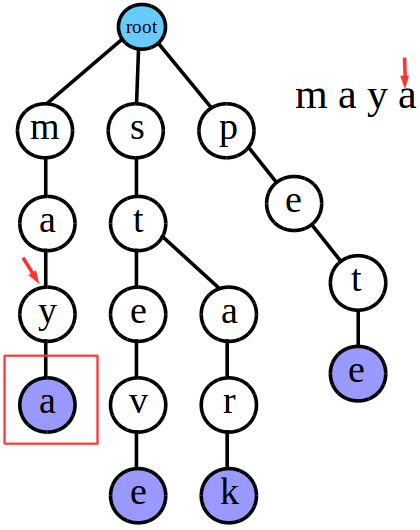
字符串的每一位都匹配成功并且最后一位在Trie树中也标记了是结尾，所以可知字符串“maya”是存在于Trie树中的QWQ

接下来检索“soldier”

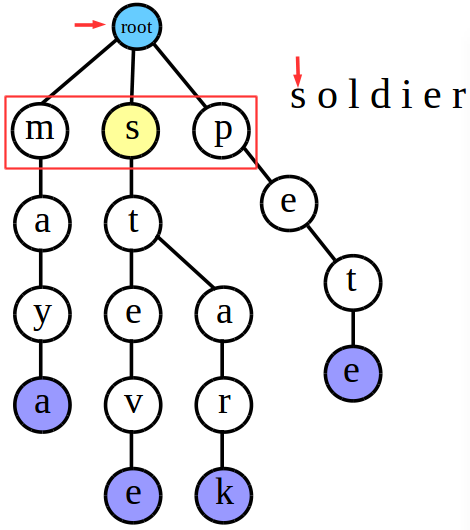
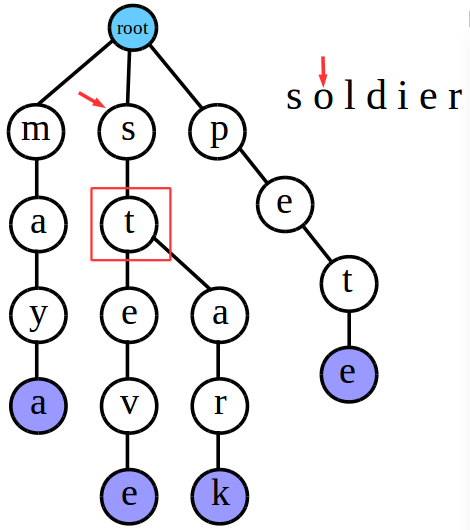
可以发现当匹配到字符串中的“o”字符时匹配失败，也就是我上面说到的第1种情况，因此可知“soldier”是不存在于Trie树中的。

最后我们来检索“pet”

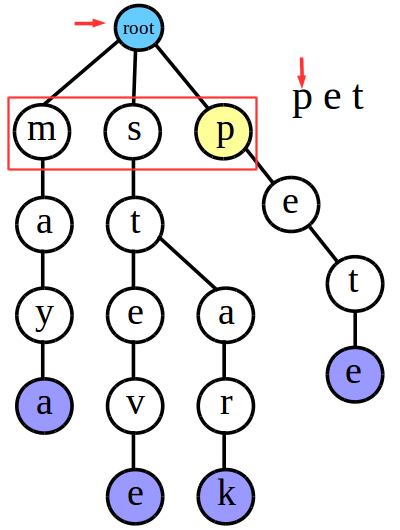
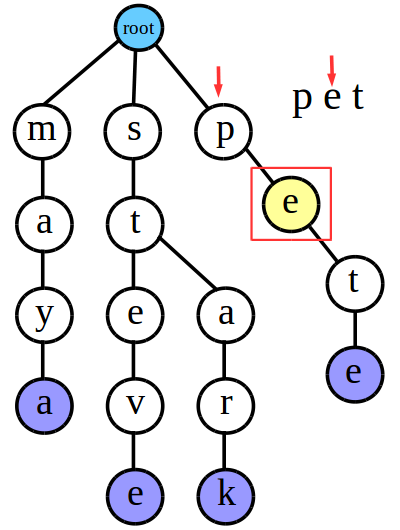
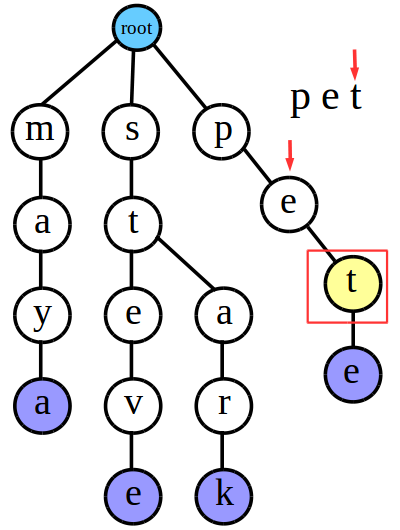
在匹配过程中，“pet”的每一个字符都匹配成功了，但是匹配到最后一位时我们发现，代表“t”字符的这个结点没有被标记为字符串的结尾，这对应了我上面说到的第2种情况，所以最后可知“pet”也是不存在于Trie树中的。

好啦就是酱紫……我放了一份代码啦！

bool exist(string s){//s是要检索的字符串
    int len=s.length();
    int now=;//从根结点(编号为0)开始
    for(int i=;i<len;i++){//逐位匹配
        if(!Trie[now].son[s[i]-'a']) return ;
        now=Trie[now].son[s[i]-'a'];
    }
    if(Trie[now].end) return ;
    else return ;
}