2D空间中求两圆的交点

出处：https://stackoverflow.com/questions/19916880/sphere-sphere-intersection-c-3d-coordinates-of-collision-points

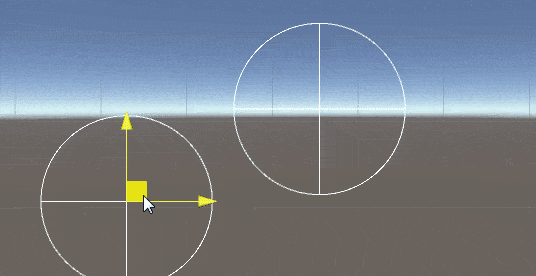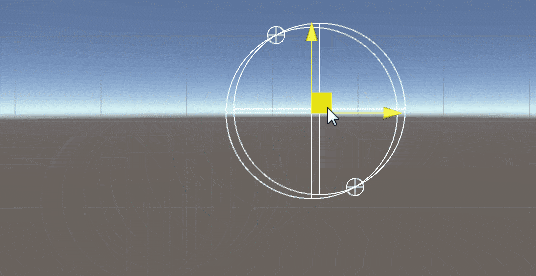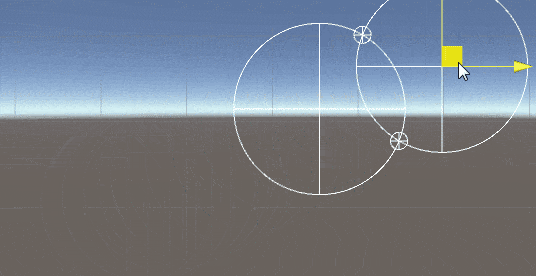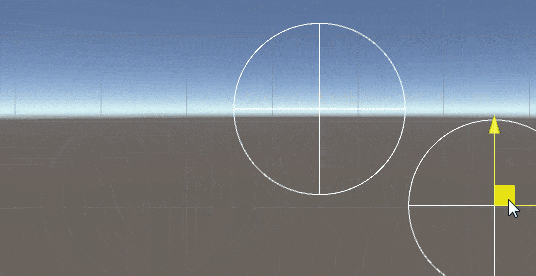
修改(加入包含和不相交情况的判断)：

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class CircleIntersect : MonoBehaviour
{
    public Transform circleA;
    public float radiusA = 1f;
    public Transform circleB;
    public float radiusB = 1f;

    public bool CalculateCircleIntersect(Vector3 c1p, Vector3 c2p, float c1r, float c2r, out Vector3 p0, out Vector3 p1)
    {
        //c1p = circle one position
        //c1r = circle one radius

        var P0 = c1p;
        var P1 = c2p;

        float d, a, h;
        p0 = Vector3.zero;
        p1 = Vector3.zero;

        d = Vector3.Distance(P0, P1);

        if (d > c1r + c2r) return false;
        if (Vector3.Distance(c2p, c1p) + c1r < c2r) return false;
        if (Vector3.Distance(c2p, c1p) + c2r < c1r) return false;

        a = (c1r * c1r - c2r * c2r + d * d) / ( * d);

        h = Mathf.Sqrt(c1r * c1r - a * a);

        Vector3 P2 = (P1 - P0);
        P2 = (P2 * (a / d));
        P2 = (P2 + P0);

        float x3, y3, x4, y4 = ;

        x3 = P2.x + h * (P1.y - P0.y) / d;
        y3 = P2.y - h * (P1.x - P0.x) / d;

        x4 = P2.x - h * (P1.y - P0.y) / d;
        y4 = P2.y + h * (P1.x - P0.x) / d; ;

        //out parameters for a line renderer
        p0 = new Vector3(x3, y3, );
        p1 = new Vector3(x4, y4, );

        return true;
    }

    void OnDrawGizmos()
    {
        if (circleA == null || circleB == null) return;

        var cacheColor = Gizmos.color;

        var p0 = default(Vector3);
        var p1 = default(Vector3);
        var isIntersect = CalculateCircleIntersect(circleA.position, circleB.position, radiusA, radiusB, out p0, out p1);

        if (isIntersect)
        {
            Gizmos.DrawWireSphere(p0, 0.1f);
            Gizmos.DrawWireSphere(p1, 0.1f);
            Gizmos.color = Color.red;
        }

        Gizmos.DrawWireSphere(circleA.position, radiusA);
        Gizmos.DrawWireSphere(circleB.position, radiusB);

        Gizmos.color = cacheColor;
    }
}