python二叉树的深度遍历之先序遍历流程图
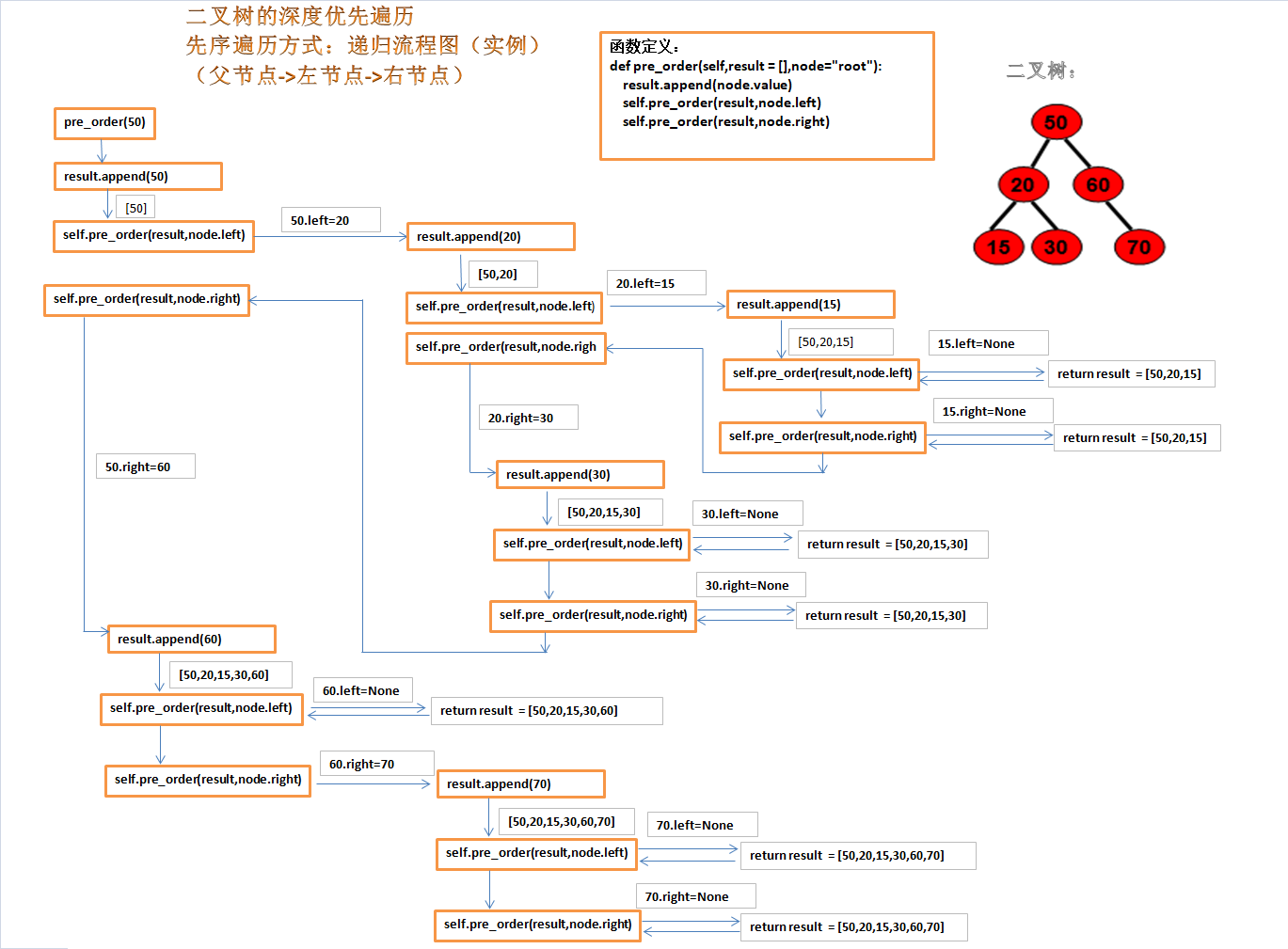
python二叉树的深度遍历之先序遍历流程图的更多相关文章
- python数据结构之树和二叉树(先序遍历、中序遍历和后序遍历)
python数据结构之树和二叉树(先序遍历.中序遍历和后序遍历) 树 树是\(n\)(\(n\ge 0\))个结点的有限集.在任意一棵非空树中,有且只有一个根结点. 二叉树是有限个元素的集合,该集合或 ...
- 【算法编程 C++ Python】根据前序遍历、中序遍历重建二叉树
题目描述 输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树.假设输入的前序遍历和中序遍历的结果中都不含重复的数字.例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7, ...
- 小小c#算法题 - 11 - 二叉树的构造及先序遍历、中序遍历、后序遍历
在上一篇文章 小小c#算法题 - 10 - 求树的深度中,用到了树的数据结构,树型结构是一类重要的非线性数据结构,树是以分支关系定义的层次结构,是n(n>=0)个结点的有限集.但在那篇文章中,只 ...
- 二叉树中序遍历,先序遍历,后序遍历(递归栈,非递归栈,Morris Traversal)
例题 中序遍历94. Binary Tree Inorder Traversal 先序遍历144. Binary Tree Preorder Traversal 后序遍历145. Binary Tre ...
- 二叉树:前序遍历、中序遍历、后序遍历,BFS,DFS
1.定义 一棵二叉树由根结点.左子树和右子树三部分组成,若规定 D.L.R 分别代表遍历根结点.遍历左子树.遍历右子树,则二叉树的遍历方式有 6 种:DLR.DRL.LDR.LRD.RDL.RLD.由 ...
- lintcode :前序遍历和中序遍历树构造二叉树
解题 前序遍历和中序遍历树构造二叉树 根据前序遍历和中序遍历树构造二叉树. 样例 给出中序遍历:[1,2,3]和前序遍历:[2,1,3]. 返回如下的树: 2 / \ 1 3 注意 你可以假设树中不存 ...
- lintcode: 中序遍历和后序遍历树构造二叉树
题目 中序遍历和后序遍历树构造二叉树 根据中序遍历和后序遍历树构造二叉树 样例 给出树的中序遍历: [1,2,3] 和后序遍历: [1,3,2] 返回如下的树: 2 / \ 1 3 注意 你可 ...
- java编写二叉树以及前序遍历、中序遍历和后序遍历 .
/** * 实现二叉树的创建.前序遍历.中序遍历和后序遍历 **/ package DataStructure; /** * Copyright 2014 by Ruiqin Sun * All ri ...
- L2-006 树的遍历 (25 分) (根据后序遍历与中序遍历建二叉树)
题目链接:https://pintia.cn/problem-sets/994805046380707840/problems/994805069361299456 L2-006 树的遍历 (25 分 ...
- 【C++】根据二叉树的前序遍历和中序遍历重建二叉树并输出后续遍历
/* 现在有一个问题,已知二叉树的前序遍历和中序遍历: PreOrder:GDAFEMHZ InOrder:ADEFGHMZ 我们如何还原这颗二叉树,并求出他的后序遍历 我们基于一个事实:中序遍历一定 ...
随机推荐
- MySQL Community Server 8.0.11下载与安装配置
一.下载 1.选择合适的安装包,我在这里下载的是目前最新的安装包,8.0.11,而且我选择下载的是解压版的,安装版的话,安装会比较麻烦. MySQL Community Server下载链接:http ...
- 第三节:Windows下检出项目和提交项目
1.将项目下载到本地: 2.在客户端中,右键点击test,选择show in explorer: 然后修改日志文件并保存: 3.在客户端中填写备注并提交: 4.提交到github中:
- 20170915 shell
1.什么是Shell 一种电脑程序与文本文件,利用Shell 可以进行系统管理,文件操作等. 2.认识bash 这个Shell 由于管理整个计算机硬件的其实是操作系统的内核(kernel),用户一般都 ...
- 如何为DigitalOcean上的服务器配置SSH密钥
本指南适用于mac OS和Linux,windows用户请绕道. 通常,当你启动DigitalOcean droplets时,只要过程完成,你会收到一封电子邮件,让你知道droplets的IP地址和密 ...
- vue-cli 3.x脚手架配置并使用vux
https://blog.csdn.net/Honnyee/article/details/82181620
- HBase学习总结(1)
HBase是一种数据库:HadoopDatabase顾名思义就是Hadoop数据库,它是一种基于hadoop文件系统HDFS的一种分布式数据库,专门设计用来快速随机读写大规模数据.本文介绍HBase的 ...
- python接口测试-登录
终于调同登录接口了 import requests import json import unittest import HTMLTestRunner ur1='http://118.178.247. ...
- canvas原生js写的贪吃蛇
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/ ...
- 解决mysql的内存表“table is full”错误
最后参考http://blog.sina.com.cn/s/blog_6942a1590101429h.html 来解决,摘录下核心 后来GOOGLE得知,需要重建该表才可以. 1. 设置新的参数 m ...
- python filter函数应用,过滤字符串
>>> candidate = 'dade142.;!0142f[.,]ad' >>> filter(str.isdigit, candidate) #保留数字 ' ...
