CRF基础知识以及如何实现Learning，Inference

CRF:Conditional Random Field，即条件随机场。

首先介绍一下基础背景知识。机器学习中的分类问题可以分为硬分类和软分类。硬分类常见的模型有SVM、PLA、LDA等。SVM可以称为max margin classifier，基于几何间隔进行分类。软分类一般分为logistic Regnesstion（概率判别模型）和 Naive Bayes（概率生成模型）。概率判别模型和概率生成模型的区别是，概率判别模型是对\(P\left ( y|x \right )\)进行建模，概率生成模型是对\(P\left ( x,y \right )\)进行建模。

1.概率生成模型

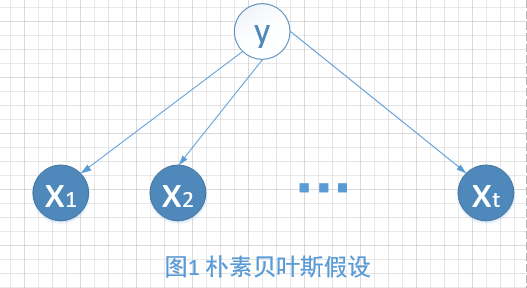
Naive即朴素贝叶斯假设，公式表示就是\(P\left ( x|y=y_{0} \right )= \prod_{i=1}^{p}P\left ( x_{i}|y=y_{0} \right )\),通俗的解释就是给定隐变量的条件下，观测变量之间相互独立，即\(x_{i}\perp x_{j}|y,i\neq j\)，如图1所示。当\(y\)被观测时，阻断了观测变量之间的路径。



当隐变量一个line的时候，就是HMM(Hidden markov model)模型，如图2所示。



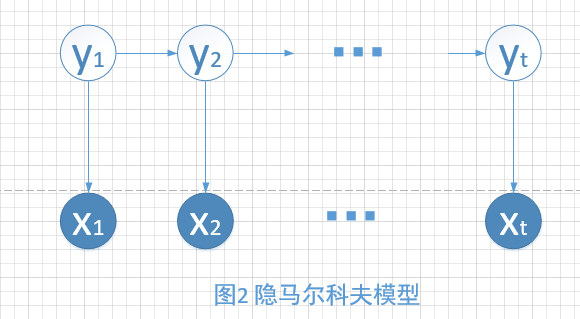
如果大家有学过概率图模型的话，肯定知道有向图中的d-分离。通过有向图的独立性假设，我们可以非常直观的得到HMM的两大假设。即齐次Markov假设和观测独立假设。这两个假设的表达式分别为：

齐次Markov假设：\(P\left ( y_{t}|y_{1:t-1},x_{1:t-1} \right )= P\left ( y_{t}|y_{t-1} \right )\)

观测独立假设：\(P\left ( x_{t}|y_{1:t},x_{1:t-1} \right )= P\left ( x_{t}|y_{t} \right )\)

2.概率判别模型

比如最大熵模型，采用最大熵思想。比如：给定方差和均值，高斯分布熵最大。。

3.两者结合就出现了MEMM:Maximum Entropy Markov Model。这是一种概率判别模型。



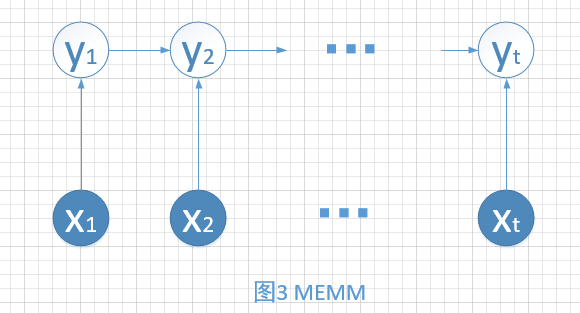
进行独立性分析可以发现，该模型打破了HMM的观测独立假设，模型变得更加的合理了。比如，文本标注问题中，上下文对于标注会产生影响。

但是同样存在标注偏差问题，原因是局部归一化。John Lafferty的论文中讲解了该问题为什么存在。用一句话来概括就是：Conditional distribution with low entropy take less notice of observation.

4.Chain-structure CRF

该模型克服了标注偏差问题，CRF的模型如下图4所示，隐变量之间变为无向边，所以是全局归一化。



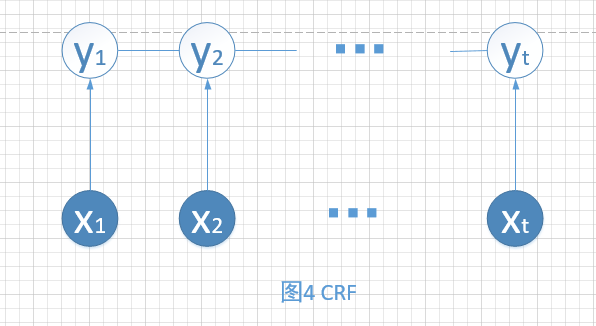
接下来会写如何利用CRF实现Learning、Inference等任务。