[NOIP2019] 划分

题目

题解

首先YY一个最简单的dp

$dp[i][j]=min(dp[j][k]+(sum[i]-sum[j])^2 (sum[i]-sum[j]>=sum[j]-sum[k])$

$dp[i][j]$表示i为终点，j为上一段起点的最小代价。

上述过程其实就是在i的左端寻找满足条件的点，然后一一计算代价并取最小值（注意这些点可能不是连续的）

但其实，我们只要取最右边的满足条件的点来更新就行了，证明见下

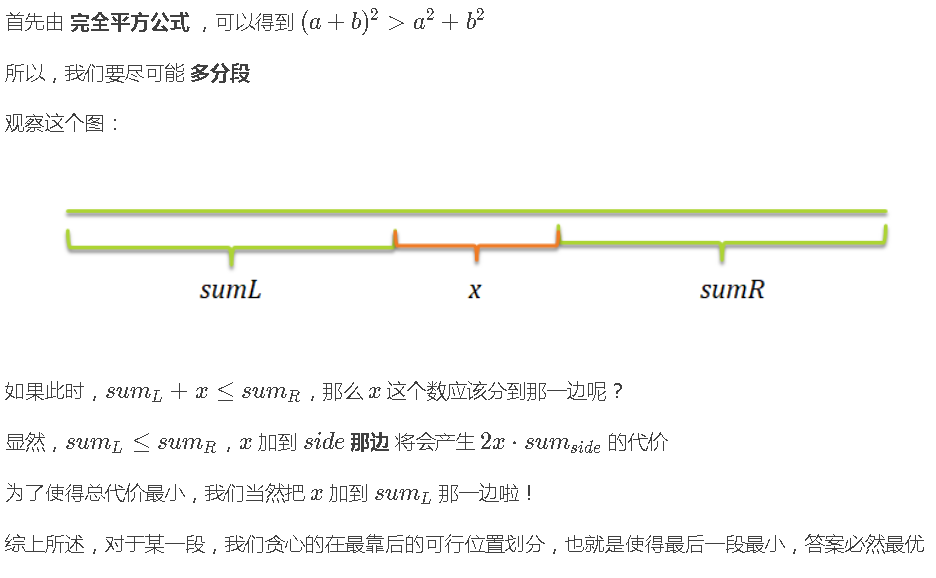
我们可以记一个$pre[i]$表示i点上一个区间的终点

这样我们就有了一个$O(n^2)$ dp

对于每个点i，我们从i往前扫，找到第一个满足 $(sum[i]-sum[j]>=sum[j]-sum[pre[j])$ 的点j ，则

$dp[i]=dp[j]+(sum[i]-sum[j])^2$

注意到如果一个点j满足i,那么它肯定满足i+1,

如果不满足i,也可能满足i+1

另外，对于 $sum[i]-sum[j]>=sum[j]-sum[pre[j]$

可以变形成 $sum[i]>=2*sum[j]-sum[pre[j]$

那么可以设一个$d(j)=2*sum[j]-sum[pre[j]$

我们可以用一个单调队列来维护满足条件的点

因为我们只需要最右边满足条件的点，所以每次i递增的时候，如果队头下一位也满足条件，就把队头踢掉（因为下一位肯定比队头更右）

然后用队头更新这一位的dp值

然后把这一位从队尾插入，并把前面d值大于它的点全部删除

这样就可以做到$O(n)$了

代码

这个是88分的，100分的要写高精，但正确性是有的。

#include <iostream>
#include <cstdio>
#define int long long
using namespace std;
#define N 4*(int)1e7+10
int sum[N],pre[N],q[N],dp[N],l=1,r=0;
#define val(a) (2*sum[a]-sum[pre[a]])
signed main()
{
	int n,type;
	cin>>n>>type;
	for(int i=1;i<=n;i++)
	{
		int a;
		scanf("%lld",&a);
		sum[i]=sum[i-1]+a;
	}
	q[++r]=0;
	for(int i=1;i<=n;i++)
	{
		while(l<r&&val(q[l+1])<=sum[i]) l++;
		pre[i]=q[l];
		dp[i]=dp[pre[i]]+(sum[i]-sum[pre[i]])*(sum[i]-sum[pre[i]]);
		while(l<=r&&val(i)<=val(q[r])) r--;
		q[++r]=i;
	}
	cout<<dp[n];
}