JAVA递归算法及经典递归例子 对于这个汉诺塔问题

前言：递归（recursion）：递归满足2个条件
    1）有反复执行的过程（调用自身）
    2）有跳出反复执行过程的条件（递归出口）
第一题：汉诺塔

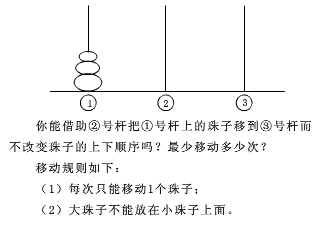
对于这个汉诺塔问题，在写递归时，我们只需要确定两个条件：

1.递归何时结束？

2.递归的核心公式是什么？即：

怎样将n个盘子全部移动到C柱上？

即：若使n个盘子全部移动到C柱上，上一步应该做什么？

​
代码实现
package diguui;

public class digui1 {

	public static void hanoi(int n,int p1,int p2,int p3)
	{
		if(1==n)
			System.out.println("盘子从"+p1+"移到"+p3);
		else
		{
			hanoi(n-1,p1,p3,p2);

			System.out.println("盘子从"+p1+"移到"+p3);

			hanoi(n-1,p2,p1,p3);
		}
	}
	public static void main(String[] args) {
		/*4表示盘数，1表示开始柱子，2表示开始柱子，3表示开始柱子*/
        hanoi( 4, 1, 2, 3);
	}

}
效果图

第二题：一般而言，兔子在出生两个月后，就有繁殖能力，一对兔子每个月能生出一对小兔子来。如果所有兔子都不死，那么一年以后可以繁殖多少对兔子？
  分析如下：

  第一个月小兔子没有繁殖能力，所以还是一对；

  两个月后，生下一对小兔子，总数共有两对；

  三个月以后，老兔子又生下一对，因为小兔子还没有繁殖能力，总数共是三对；

  ……　

  依次类推可以列出下表：

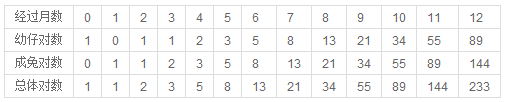
可以得出：

  斐波纳契数列，又称黄金分割数列，指的是这样一个数列：1、1、2、3、5、8、13、21、……

  这个数列从第三项开始，每一项都等于前两项之和。

package diguui;

public class digui1 {

	public static int fun(int m){
		if(m<2){
			return 1;
		}else{
			return fun(m - 1)+fun(m-2);
		}
	}
	public static void main(String[] args) {

        System.out.println(fun(12));
	}

}