Optimal binary search trees

问题

该问题的实际应用

Suppose that we are designing a program to translate text from English to French. For each occurrence of each English word in the text, we need to look up its French equivalent. We could perform these lookup operations by building a binary search tree with n English words as keys and their French equivalents as satellite data.

Because we will search the tree for each individual word in the text, we want the total time spent searching to be as low as possible. We could ensure an O(lg n) search time per occurrence by using a red-black tree or any other balanced binary search tree.

Words appear with different frequencies, however, and a frequently used word such as the may appear far from the root while a rarely used word such as machicolation appears near the root. Such an organization would slow down the translation, since the number of nodes visited when searching for a key in a binary search tree equals one plus the depth of the node containing the key. We want words that occur frequently in the text to be placed nearer the root.

Moreover, some words in the text might have no French translation, and such words would not appear in the binary search tree at all. How do we organize a binary search tree so as to minimize the number of nodes visited in all searches, given that we know how often each word occurs?(被给定时间相同)

该问题涉及的概念以及特点

an optimal binary search tree，其概念如下：

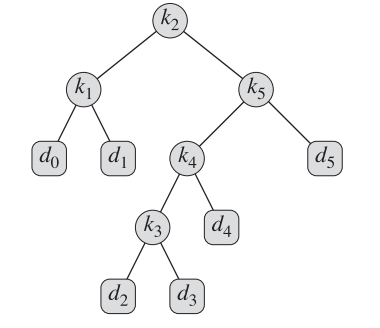
• we are given a sequence K = { k₁, k₂, ... , k_n } of n distinct keys in sorted order (so that k₁< k₂< ... < k_n), and we wish to build a binary search tree from these keys. For each key ki , we have a probability pi that a search will be for k_i.

• Some searches may be for values not in K, and so we also have n + 1 “dummy keys” d₀, d₁, ... , d_n representing values not in K. For each dummy key d_i , we have a probability q_i that a search will correspond to d_i .

• In particular, d₀ represents all values less than k₁, dn represents all values greater than k_n,and for i = 1, 2, ... , n-1, the dummy key d_i represents all values between k_i and k_i+1.

• 

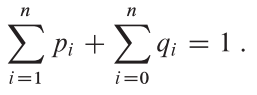
• Each key k_i is an internal node, and each dummy key d_i is a leaf.

• the expected cost of a search in an binary search tree T is：

  

问题形式化定义

Input:

• { k₁, k₂, ... , k_n } && { p₁, p₂, ... , p_n }

• { d₀, d₁, ... , d_n } && { q₀, q₁, ... , q_n }

Output

• an optimal binary search tree

暴力算法或其他可行算法分析

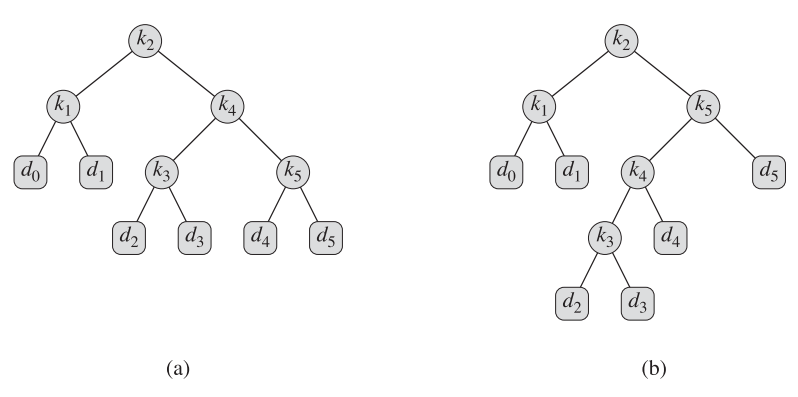
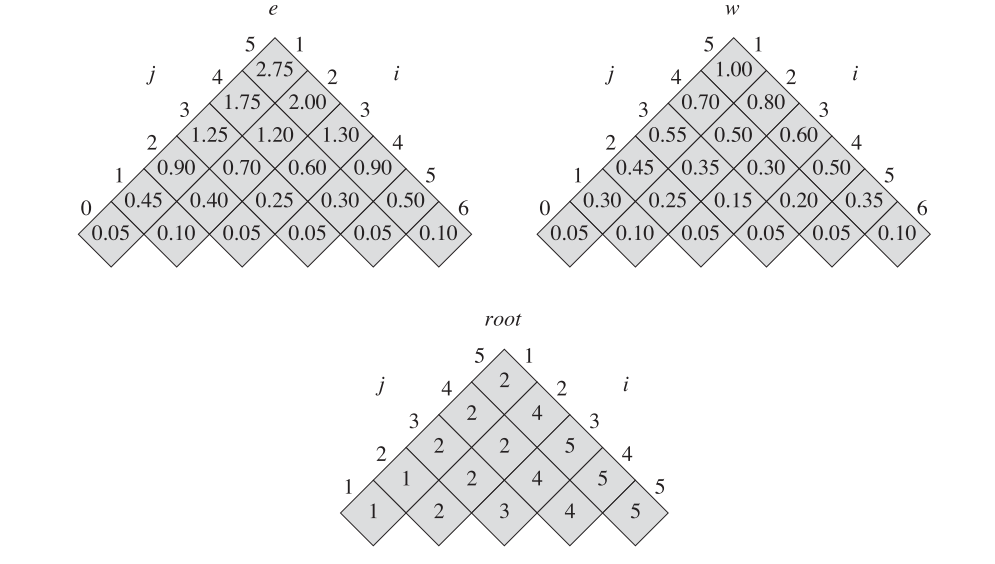
Figure 15.9(b) shows an optimal binary search tree for the probabilities given in the figure caption; its expected cost is 2.75. Figure 15.9(b)'s cost is 2.80

This example shows that an optimal binary search tree is not necessarily a tree whose overall height is smallest. Nor can we necessarily construct an optimal binary search tree by always putting the key with the greatest probability at the root.

We can label the nodes of any n-node binary tree with the keys k1;k2; :::; kn to construct a binary search tree, and then add in the dummy keys as leaves. In Problem 12-4, we saw that the number of binary trees with n nodes is Ω(4ⁿ/n^3/2), and so we would have to examine an exponential number of binary search trees in an exhaustive search. Not surprisingly, we shall solve this problem with dynamic programming.

动态规划解法

优化子结构

Theorem (Optimal substructure of Optimal binary search trees)

if an optimal binary search tree T has a subtree T' containing keys k_i ... k_j , then this subtree T' must be optimal as well for the subproblem with keys k_i ... k_j and dummy keys d_i-1 ... d_j.

Proof

If there were a subtree T00 whose expected cost is lower than that of T0, then we could cut T0 out of T and paste in T00, resulting in a binary search tree of lower expected cost than T, thus contradicting the optimality of T.

DETAIL

There is one detail worth noting about “empty” subtrees. Suppose that in a subtree with keys k_i ... k_j , we select k_i as the root. By the above argument, k_i ’s left subtree contains the keys k_i ... k_i-1. We interpret this sequence as containing no keys. Bear in mind, however, that subtrees also contain dummy keys. We adopt the convention that a subtree containing keys k_i ... k_i-1 has no actual keys but does contain the single dummy key d_i-1. Symmetrically, if we select k_j as the root, then k_j ’s right subtree contains the keys k_j-1 ,..., k_j ; this right subtree contains no actual keys, but it does contain the dummy key d_j .

子问题重叠性

We need to use the optimal substructure to show that we can construct an optimal solution to the problem from optimal solutions to subproblems. Given keys k_i ... k_j , one of these keys, say k_r (i <= r <= j ), is the root of an optimal subtree containing these keys. The left subtree of the root kr contains the keys k_i ,..., k_r-1 (and dummy keys d_i-1 ,..., d_r-1), and the right subtree contains the keys k_r+1 ,..., k_j (and dummy keys d_r ,.., d_j ). As long as we examine all candidate roots k_r,where i <= r <= j , and we determine all optimal binary search trees containing k_i ,..., k_r-1 and those containing k_r+1 ,.., k_j , we are guaranteed that we will find an optimal binary search tree.

以上文字说明了此问题的最优解构建其实与矩阵链乘问题的最优解的构建基本类似。那么自然可以论证其子问题优化解的存在。

递归的定义优化解的代价

Let us define e[i, j] as the expected cost of searching an optimal binary search tree containing the keys k_i ... k_j .

基准情况十分简单：

• The easy case occurs when j = i - 1. Then we have just the dummy key d_i-1. The expected search cost is e[i, i - 1] = q_i-1.

其他情况的论述：

When j >= i , we need to select a root k_r from among k_i ... k_j and then make an optimal binary search tree with keys k_i ,..., k_r-1 as its left subtree and an optimal binary search tree with keys k_r+1 ,..., k_j as its right subtree.

What happens to the expected search cost of a subtree when it becomes a subtree of a node? The depth of each node in the subtree increases by 1. So:

最后的递归解的表示：

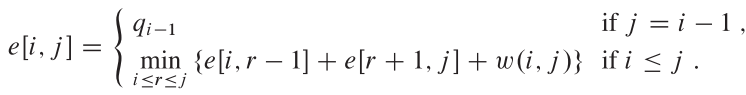
计算优化解的代价算法

we store the e[i, j] values in a table e[1...n+1 , 0...n]. The first index needs to run to n-1 rather than n because in order to have a subtree containing only the dummy key d_n, we need to compute and store e[n + 1, n]. The second index needs to start from 0 because in order to have a subtree containing only the dummy key d₀, we need to compute and store e[1, 0].

这里对于矩阵边界的理解，十分精辟，建议结合图示进行观看，可以帮助理解。

下面将说明 w[i, j]的构建以及递归方程。

We will need one other table for efficiency. Rather than compute the value of w[i, j] from scratch every time we are computing e[i, j] —which would take Θ(j - i) additions—we store these values in a table w[1 .. n + 1, 0 ... n].

• For the base case, we compute w[i, i - 1] = q_i-1 for 1 <= i <= n + 1.
• For j >= i,we compute : w[i, j] = w[i, j - 1] + p_j + q_j.

空间结构：
M[1:n+1; 0:n]: 存储优化解搜索代价
W[1: n+1; 0:n]: 存储代价增量Wm(i, j)
Root[1:n; 1:n]: root(i, j)记录子问题{ki, …, kj}优化解的根

Optimal-BST(p, q, n)
 For  i=1  To  n+1   Do
      E(i, i-1) = qi-1;
      W(i, i-1) = qi-1;
 For  l=1  To  n   Do
      For   i=1   To   n-l+1   Do
            j=i+l-1;
            E(i, j)=正无穷;
            W(i, j)=W(i, j-1)+pj+qj;
            For  r=i  To  j   Do
                 t=E(i, r-1)+E(r+1, j)+W(i, j);
                 If    t<E(i, j)
                 Then  E(i, j)=t;
                          Root(i, j)=r;
 Return  E and  Root    　

Eg:

构造最优解的算法

最终的最优解将采用如下形式进行输出，其形式对应于上面所给例子。

伪代码为：

CONSTRUCT-OPTIMAL-BST(root)
n = root[0].length
print K {root[1,n]} is the root
Print-BST(root,1,n)

Print-BST(root,i,j)
if (i <= root[i,j]-1)
   print k {root[i,root[i,j]-1]} is the left child of k {root[i,j]}
   print-BST(root,i,root[i,j]-1)
else
   print d {root[i,j]-1} is the left child of k {root[i,j]}
if (j >= root[i,j]+1)
   print K {root[root[i,j]+1,j]} is the right child of K {root[i,j]}
   print-BST(root,root[i,j]+1,j)
else
   print d {j} is the right child of k {root[i,j]}

算法复杂度说明

时间复杂度：

• 计算代价的时间：O(n³).

The OPTIMAL-BST procedure takes O(n³) time, just like MATRIX-CHAINORDER. We can easily see that its running time is O(n³), since its for loops are nested three deep and each loop index takes on at most n values.

The loop indices in OPTIMAL-BST do not have exactly the same bounds as those in MATRIX-CHAINORDER, but they are within at most 1 in all directions. Thus, like MATRIX-CHAINORDER, the OPTIMAL-BST procedure takes Ω(n³) time.

算法代码

#include<stdio.h>
#include<string.h>

#define N 5
#define MAX_FLOAT 10.0

void OPTIMAL_BEST(float* p, float* q, int n);
void CONSTRUCT_OPTIMAL_BST(int root[N + 1][N + 1]);
void Print_BST(int root[N + 1][N + 1], int i, int j);

void main() {
	float p[N + 1] = { 0.0,0.15,0.10,0.05,0.10,0.20 };
	float q[N + 1] = { 0.05,0.10,0.05,0.05,0.05,0.10 };
	OPTIMAL_BEST(p, q, N);

}
void OPTIMAL_BEST(float* p, float* q, int n) {
	float e[N + 2][N + 1];
	float w[N + 2][N + 1];
	int root[N + 1][N + 1];
	memset(e, 0.0, sizeof(float) * (N + 2) * (N + 1));
	memset(w, 0.0, sizeof(float) * (N + 2) * (N + 1));
	memset(root, 0, sizeof(int) * (N + 1) * (N + 1));
	for (int i = 1; i <= n + 1; i++) {
		e[i][i - 1] = q[i - 1];
		w[i][i - 1] = q[i - 1];
	}
	for (int l = 1; l <= n; l++) {
		for (int i = 1; i <= n - l + 1; i++) {
			int j = i + l - 1;
			e[i][j] = MAX_FLOAT;
			w[i][j] = w[i][j - 1] + p[j] + q[j];
			for (int r = i; r <= j; r++) {
				float t = e[i][r - 1] + e[r + 1][j] + w[i][j];
				if (t < e[i][j]){
					e[i][j] = t;
					root[i][j] = r;
				}
			}
		}
	}
	for (int i = 1; i <= n + 1; i++) {
		for (int j = 0; j <= n; j++) {
			printf("%.2f	", e[i][j]);
		}
		printf("\n");
	}
	printf("\n");
	printf("\n");
	printf("\n");
	for (int i = 1; i <= n + 1; i++) {
		for (int j = 0; j <= n; j++) {
			printf("%.2f	", w[i][j]);
		}
		printf("\n");
	}
	printf("\n");
	printf("\n");
	printf("\n");
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			printf("%d	", root[i][j]);
		}
		printf("\n");
	}
	printf("\n");
	printf("\n");
	printf("\n");
	CONSTRUCT_OPTIMAL_BST(root);
}

void CONSTRUCT_OPTIMAL_BST(int root[N + 1][N + 1]) {
	printf("K %d is the root\n", root[1][N]);
	Print_BST(root, 1, N);
}

void Print_BST(int root[N + 1][N + 1], int i, int j) {
	if (i <= (root[i][j] - 1)) {
		printf("k %d is the left child of k %d\n", root[i][root[i][j] - 1], root[i][j]);
		Print_BST(root, i, root[i][j] - 1);
	}
	else {
		printf("d %d is the left child of k %d\n", root[i][j] - 1, root[i][j]);
	}
	if (j >= root[i][j] + 1) {
		printf("k %d is the rightchild of k %d\n", root[root[i][j] + 1][j], root[i][j]);
		Print_BST(root, root[i][j] + 1, j);
	}
	else {
		printf("d %d is the right child of k %d\n", j, root[i][j]);
	}
}