CF535E Tavas and Pashmaks 单调栈、凸包

传送门

题意：有一场比赛，$N$个人参加。每个人有两种参数$a,b$，如果存在正实数$A,B$使得$\frac{A}{a_i} + \frac{B}{b_i}$在$i=x$处取得最大值（可以有多个最大值），则称选手$x$可以夺冠。问共有多少人能够夺冠。$N \leq 2 \times 10^5 , 1 \leq a , b \leq 10^4$

---

考虑将$(\frac{1}{a_i},\frac{1}{b_i})$看做平面上的点，我们的目标就是在这些点上求目标函数$z=Ax+By$的最小值（线性规划），而对于每一条这样的直线，都一定是与某一个凸包切于一个点或与这个凸包中的某条线重合。可以考虑到这就是若干$(\frac{1}{a_i},\frac{1}{b_i})$的点构成的左下凸包（也就是一个完整凸多边形的左下部分）。将点从大到小排序之后使用单调栈维护凸包即可。

有一个很重要的剪枝：当$a_i \leq a_j , b_i \leq b_j$时，$i$号无需计算

还要注意$a,b$相同的人的计算。

UPD：似乎上面很抽象，画个图解释一下

我们把上面的剪枝做完之后，得到的所有点的坐标横坐标递增，纵坐标递减，且都分布在第一象限。

画在图上就是这样子：

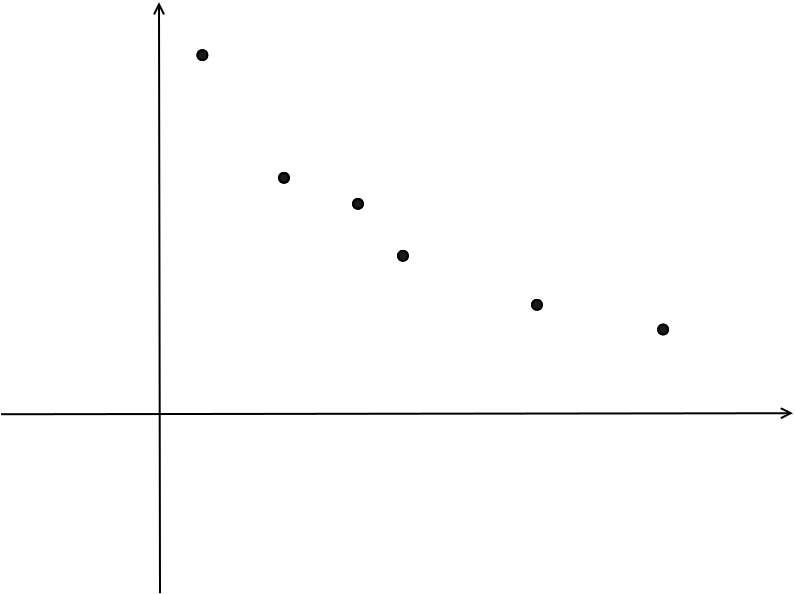
话说Dia画点竟然要用圆形填充，所以点会很大

我们考虑这些点在$z=Ax + By$的目标函数上的最小取值（也就是取一个点带入函数中，使得$z$最小）。

先说结论：不论$A,B$如何取值，最小值一定在下图图形中连上的点上取到。

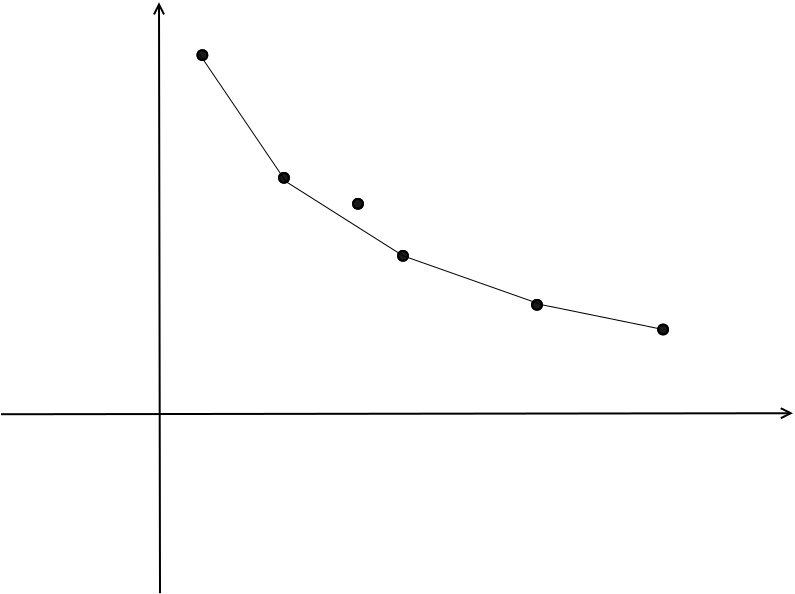
那么为什么中间那个没连上的点不能取到最优解呢？

我们按照斜率绝对值从大到小观察选点情况，可以知道随着斜率绝对值变小，选择的点的横坐标会不断增加，一个点会成为最优解对应的斜率范围会是一段区间，也就是当斜率越过这个点对应的最优解区间之后，这个点一定不会对最优解产生贡献了。

那么我们考虑在什么情况下最优解会从一个点转移到另一个点。

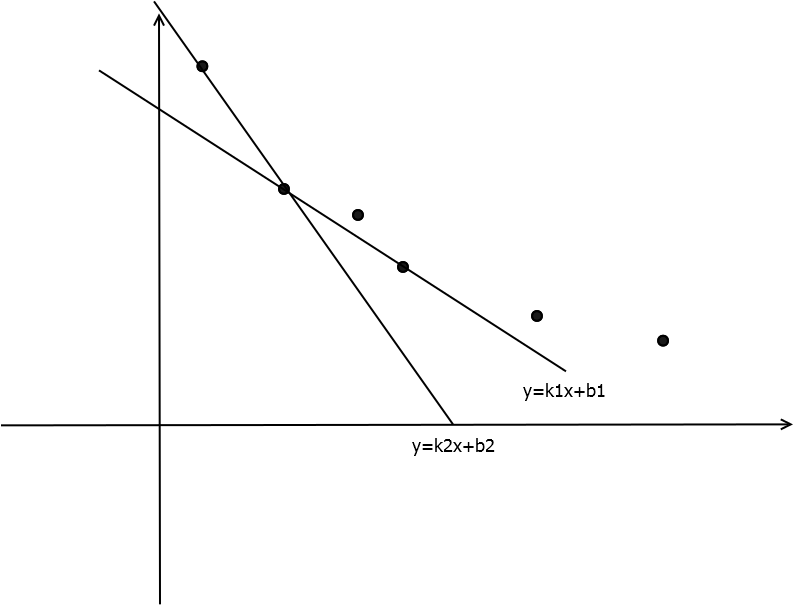
我们将点从左往右编号。考虑上面两条直线。可以知道当直线的斜率在$[k2,k1]$范围内时，$2$号点会产生最优解，而当$k=k1$时，$4$号点也会产生最优解，而当$k \geq k1$时，最优解就会从$2$号点转移为$4$号点了。

所以我们可以发现，最优解转移时直线的斜率就是这两个点之间的斜率。

接下来我们考虑如何排除非最优解了。

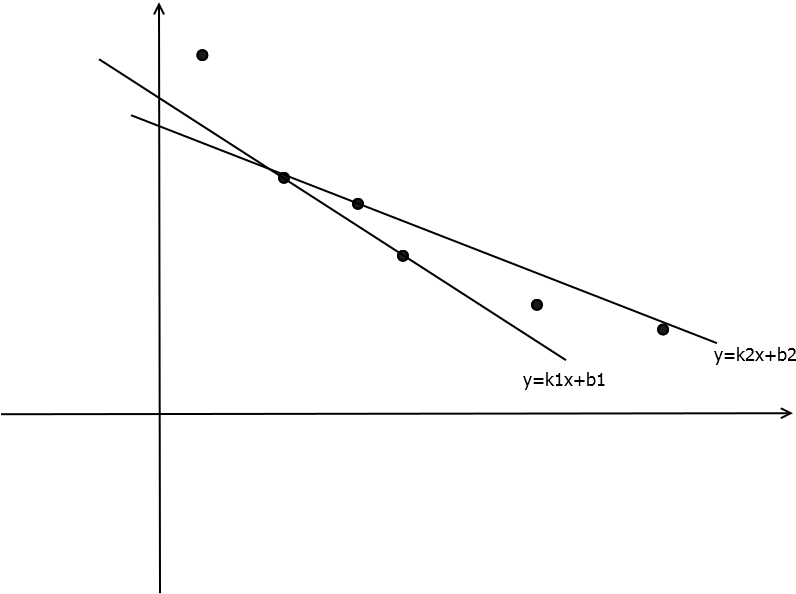
考虑上图中从$2$号点转移到$3$号点与$4$号点的情况。我们发现从$2$号点转移到$3$号点的斜率是$k2$，而从$2$号点转移到$4$号点的斜率是$k1$，且$k1 < k2$。这意味着斜率绝对值从大到小的过程中，$4$号点会比$3$号点先到达最优解转移时的斜率，所以$2$号点的最优解会先转移到$4$号点，而$3$号点无法从$2$号点转移，就是无用的节点了。

所以依据上面的研究，我们可以通过单调栈维护这样子的一个类似凸多边形的结构，模型如下：

①把$1$号点与$2$号点加入栈中

②准备加入一个新的点$i$

③考虑当前栈中是否有无用节点。我们设栈顶下标为$hd$，我们就可以考虑$Stack_{hd}$与$i$从$Stack_{hd - 1}$转移最优解时的斜率（也就是$Stack_{hd}$与$i$和$Stack_{hd - 1}$相连得到的直线的斜率），如果$i$的斜率绝对值大于$Stack_{hd}$的斜率，弹出栈顶，如果栈大小大于$1$，进入③，否则进入④

④加入当前点。如果还有新的点，进入②，否则进入⑤

⑤统计单调栈内的点，对应答案。

 #include<bits/stdc++.h>
 #define ld long double
 #define eps 1e-10
 using namespace std;

 inline int read(){
     ;
     char c = getchar();
     while(!isdigit(c))
         c = getchar();
     while(isdigit(c)){
         a = (a << ) + (a << ) + (c ^ ');
         c = getchar();
     }
     return a;
 }

 ;
 struct point{
     int a , b , ind;
 }now[MAXN];
 int nxt[MAXN] , pre[MAXN] , S[MAXN] , tl;
 bool can[MAXN];

 bool cmp(point a , point b){
     if(a.a == b.a)
         return a.b > b.b;
     return a.a > b.a;
 }

 ld calcK(point a , point b){
     return (ld)a.a * b.a * (b.b - a.b) / a.b / b.b / (b.a - a.a);
 }

 int main(){
     int N = read();
      ; i <= N ; i++){
         now[i].a = read();
         now[i].b = read();
         now[i].ind = i;
         nxt[i] = i + ;
         pre[i] = i - ;
     }
     sort(now +  , now + N +  , cmp);
     ].b;
     //双向链表排除冗余状态
      ; i <= N ; i++)
         if(now[i].b <= maxB){
             nxt[pre[i]] = nxt[i];
             pre[nxt[i]] = pre[i];
         }
         else
             maxB = now[i].b;
     S[] = ;
     tl = ;
     //通过斜率维护单调栈（与斜率优化很相似）
     ] ; i <= N ; i = nxt[i]){
          && calcK(now[i] , now[S[tl - ]]) < calcK(now[S[tl - ]] , now[S[tl - ]]))
             tl--;
         S[tl++] = i;
     }
      ; i < tl ; i++){
         can[now[S[i]].ind] = ;
         //还原原来位置相同的点
          ; j <= N && now[S[i]].a == now[j].a && now[S[i]].b == now[j].b ; j++)
             can[now[j].ind] = ;
     }
      ; i <= N ; i++)
         if(can[i])
             printf("%d " , i);
     ;
 }

---

鉴于某人说我直接蒯题解，再来更个精度易爆炸的做法

考虑$\frac{A}{a_i} + \frac{B}{b_i}$，除掉$B$可以得到一个自变量为$\frac{A}{B}$的线，将这些线用斜率优化的方式加入就可以了，实质也是维护一个凸包。但是这种做法对于精度要求很高，似乎要把斜率与截距同乘$10^9$才能保证精度（或者使用一般式）