[Web] Web请求过程之二：DNS 域名解析

一、域名解析过程

1、浏览器检查缓存，域名缓存时间可以通过 TTL 属性来设置。

2、如果浏览器缓存中没有，浏览器会去查找操作系统缓存中是否有这个域名对应的 DNS 解析结果。如果要设置域名对应的 IP 地址，可以在Windows 中的配置文件 C:\Windows\System32\drivers\etc\hosts 来设置或在 Linux 中的配置文件 /etc/hosts 来设置，操作系统会缓存这个 IP 地址。

3、如果前两步无法解析时，会把域名发给 Local DNS 服务器（本地域名服务器）。如果要查询 LocalDNS 服务器的信息，在 Windows 下可以通过 ipconfig 命令查询，在 linux 下可以通过 cat /etc/resolv.conf 文件查询。

4、如果 Local DNS 仍然没有查询到，就直接到 Root DNS 服务器（根域名服务器）请求解析。

5、Root DNS 服务器返回给 Local DNS 服务器一个所查询域的 gTLD 服务器（主域名服务器），gTLD 是国际顶级域名服务器。

6、Local DNS 服务器向 gTLD 服务器发送请求。

7、gTLD 服务器返回域名对应的域名服务器地址，即域名解析任务由这个域名提供商的服务器完成。

8、在域名服务器查询到 IP 地址，连同 TTL 值返回给 Local DNS 服务器，在 Local NDS 服务器的缓存时间由 TTL 控制。

9、将解析结果返回给用户，并根据 TTL 的值在本地系统缓存。

二、查看解析结果

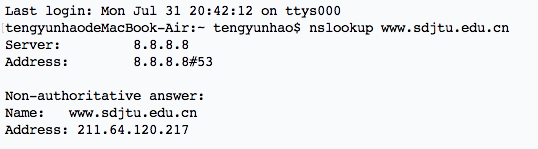
在 Linux 和 Windows 下都可以用 nslookup 命令来查询域名的解析结果，如下图。

另外在 Linux 系统中还可以使用 dig 命令来查询 DNS 解析过程。

 

 

三、清除域名缓存

域名解析后会主要在两个地方缓存结果，一个是 Local DNS 服务器，另一个是用户的本地机器。这两个缓存都是由 TTL 值和本地缓存大小控制的。在 Windows 中我们可以通过执行 ipconfig / flushdns 命令来刷新缓存，在 Linux 中我们可以通过执行 /etc/init.d/nscd restart 命令来清除缓存。

另外在 Java 的 JVM 中也会缓存 DNS 的解析结果，这个缓存是在 InetAddress类中完成的。它有两种缓存策略：一是正确解析后的结果缓存，另一种是失败的解析结果缓存。这两个缓存时间是在 %JAVA_HOME%\lib\security\java.security 文件中配置的。两个配置项分别是：networkaddress.cache.ttl 和 networkaddress.cache.negative.ttl，默认值分别为 -1（永不失效）和 10（缓存10秒）。如果使用InetAddress类解析域名必须是单例模式，否则每次创建实例时都要进行一次完整的域名解析，非常耗时。

 

四、域名解析的几种方式

域名解析记录主要分为 A 记录、MX 记录、CNAME 记录、NS 记录和 TXT 记录。

1、A 记录：即 Address，用来指定域名对应的 IP 地址。A 记录可以将多个域名解析到一个 IP 地址，但不能将一个域名解析到多个 IP 地址。

2、MX 记录：即 Mail Exchange，用来将某个域名下的邮件服务器指向自己的 Mail Server。设置之后正常 Web 请求仍然解析到 A 记录的 IP 地址，但是邮件的路由将会被解析到 MX 记录的 IP 地址。

3、CNAME 记录：即 Canonical Name（别名解析），可以为一个域名设置一个或多个别名。

4、NS 记录：为某个域名指定 DNS 解析服务器。

5、TXT 记录：为某个主机名或域名设置说明。