[NOI.AC]COUNT(数学)

解析：

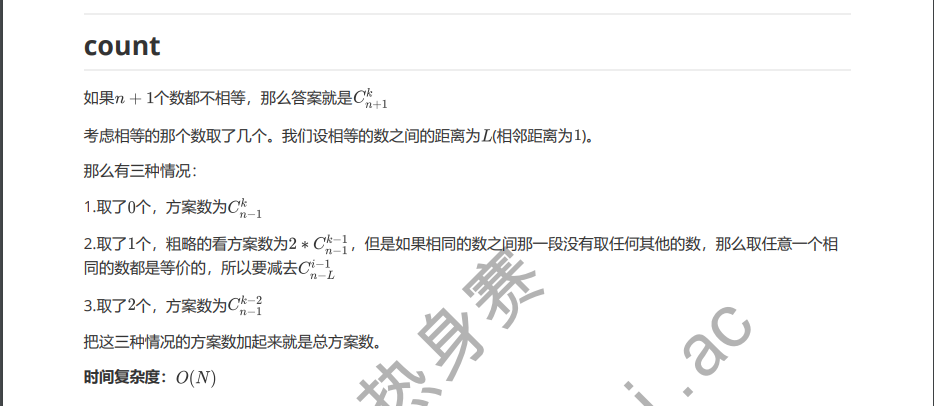
也可以将所有的可能都计算出来，后进行减法运算。

代码：

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define rint register int

inline int read(){
    int x=,f=;char ch=getchar();
    while(!isdigit(ch)) f=(ch==),ch=getchar();
    while( isdigit(ch)) x=(x<<)+(x<<)+(ch^),ch=getchar();
    return f?(~x+):x;
}

const ll md=1e9+;
#define man 100050

int n;
long long fac[man],inv[man];
int x,y,xx,yy,a[man],v[man];

inline long long bpow(long long a,int b){
    long long ans=;a%=md;
    while(b){
        if(b&) ans=ans*a%md;
        a=a*a%md;
        b>>=;
    }
    return ans;
}

inline ll C(ll nn,ll mm){
    ll ret=fac[nn]*inv[mm]%md*inv[nn-mm]%md;
    return ret%md;
}

int main(){
    n=read();
    memset(v,,sizeof(v));
    for(rint i=;i<=n+;i++){
        scanf("%d",&a[i]);
        if(v[a[i]]!=) xx=v[a[i]],yy=i;
        if(v[a[i]]==) v[a[i]]=i;

    }

    x=xx-;y=n+-yy;
    fac[]=inv[]=;
    for(rint i=;i<=n+;i++)
        fac[i]=fac[i-]*i%md,inv[i]=bpow(fac[i],md-);

    printf("%d\n",n);
    for(rint i=;i<=n;i++){
        ll ans=;
        if(x+y>=i-) ans=(C(n+,i)-C(x+y,i-)+md)%md;
        else ans=C(n+,i)%md;
        while(ans<) ans=(ans+md)%md;
        printf("%lld\n",ans);
    }
    printf("1\n");
    return ;
}